Задача 1.
Электронные часы показывают 20:11. Сколько минут пройдёт прежде, чем часы впервые покажут тот же набор цифр 0, 1, 1 и 2 в некотором другом порядке?
(А) 45
(Б) 49
(В) 50
(Г) 59
(Д) 60
Задача 2.
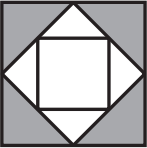
На рисунке изображены три квадрата с общим центром. Площадь самого маленького квадрата равна 6. Чему равна площадь закрашенной области?
(А) 6
(Б) 12
(В) 15
(Г) 18
(Д) 24
Задача 3.
На одной стороне улицы стоят дома с чётными номерами: 2, 4, 6, ..., а на другой стороне — с нечётными: 1, 3, 5, ... Последний дом на чётной стороне имеет номер 12, а всего на улице 17 домов. Какой номер имеет последний дом на нечётной стороне?
(А) 5
(Б) 7
(В) 13
(Г) 17
(Д) 21
Задача 4.
Значение выражения $\displaystyle \frac{2011⋅2,011}{201,1⋅20,11}$ равно
(А) 0,01
(Б) 0,1
(В) 1
(Г) 10
(Д) 100
Задача 5.
Из всех трёхзначных чисел, сумма цифр которых равна 8, выбрали самое маленькое и самое большое. Чему равна их сумма?
(А) 707
(Б) 907
(В) 916
(Г) 1000
(Д) 1001
Задача 6.
Среднее арифметическое чисел a и b равно 17, а среднее арифметическое чисел a, b и c равно 15. Чему равно c?
(А) 14
(Б) 13
(В) 12
(Г) 11
(Д) 10
Задача 7.
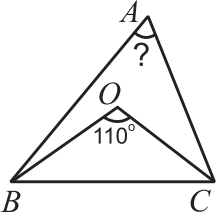
Внутри треугольника ABC выбрана точка O. Оказалось, что ∠OBC = 2∠OBA, ∠OCB = 2∠OCA и ∠BOC = 110°. Чему равен ∠BAC?
(А) 60°
(Б) 70°
(В) 75°
(Г) 80°
(Д) 100°
Задача 8.
Чему равно $(a:b):(c:d)?$
(А) $\displaystyle \frac{ad}{bc}$
(Б) $\displaystyle \frac{ac}{bd}$
(В) $\displaystyle \frac{ab}{cd}$
(Г) $\displaystyle \frac{bc}{ad}$
(Д) $\displaystyle \frac{cd}{ab}$
Задача 9.
Когда от каждого из двух чисел отняли половину меньшего из них, оказалось, что большая разность в три раза больше меньшей. Во сколько раз большее число больше меньшего?
(А) 1
(Б) 2
(В) З
(Г) 4
(Д) 5
Задача 10.
Сколькими способами к фигуре на рисунке можно добавить одну клетку так, чтобы получившаяся фигура имела ось симметрии?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 11.
Положительное число a меньше 1, а число b больше 1. Какое из следующих чисел наибольшее?
(А) a + b
(Б) ab
(В) a/b
(Г) b
(Д) невозможно определить
Задача 12.
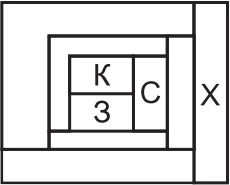
Каждую область на рисунке надо покрасить в один из четырёх цветов: красный (К), зелёный (3), синий (С) или жёлтый (Ж). Любые две области, имеющие общую границу, должны быть покрашены в разные цвета. Три области уже покрашены. Каким цветом будет покрашена область, отмеченная буквой Х?
(А) красным
(Б) синим
(В) зелёным
(Г) жёлтым
(Д) невозможно определить
Задача 13.
Дима ввёл новую операцию: a ⊗ b = ab. Если (5 ⊗ 2) ⊗ 6 = (5 ⊗ 3) ⊗ k, то k равно
(А) 3
(Б) 4
(В) 6
(Г) 8
(Д) 12
Задача 14.
Квадратный лист бумаги разделён на 6 прямоугольников (см. рисунок). Сумма периметров всех шести прямоугольников равна 120. Чему равна площадь этого листа бумаги?

(А) 48
(Б) 64
(В) 110,25
(Г) 144
(Д) 256
Задача 15.
Каждый год в день конкурса «Кенгуру» Вася несется в школу из дома бегом. В этом году ему понадобилось на дорогу на 20% меньше времени, чем в прошлом. Это значит, что его скорость возросла на
(А) 10%
(Б) 20%
(В) 25%
(Г) 50%
(Д) 100%
Задача 16.
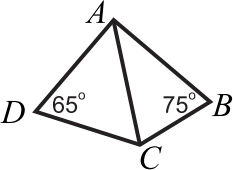
В четырёхугольнике ABCD известны углы B и D (см. рисунок). Кроме того, известно, что AB = AC и ∠BAD = 80°. Чему равен ∠BDC?
(А) 10°
(Б) 15°
(В) 20°
(Г) 30°
(Д) 45°
Задача 17.
Сторона клетки на рисунке равна 1. Сколько существует ломаных длины 5, идущих по сторонам клеток, начинающихся в узле и содержащих точки A и B?
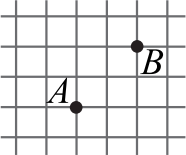
(А) 12
(Б) 24
(В) 30
(Г) 36
(Д) 54
Задача 18.
Маша выписала в ряд числа от 1 до 100, подчеркнула некоторые цифры, а потом переписала все подчеркнутые цифры в том же порядке без пробелов. Она получила строчку 20112011..., состоящую из нескольких «экземпляров» числа 2011. Какое наибольшее число этих экземпляров могло получиться?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 19.
Замкнутая ломаная на поверхности куба проходит через две вершины и середины двух рёбер (см. рисунок). Как может выглядеть развёртка этого куба?
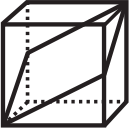
(А) 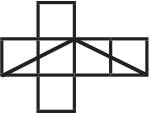
(Б) 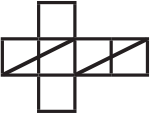
(В) 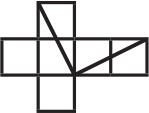
(Г) 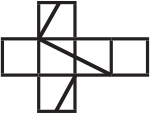
(Д) 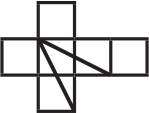
Задача 20.
По кругу пишут 6 различных чисел так, чтобы любые два соседних числа отличались на 3 или на 5. Какова наибольшая возможная разность между двумя из написанных чисел?
(А) 15
(Б) 13
(В) 11
(Г) 5
(Д) 3
Задача 21.
На плоскости нарисован отрезок AB длины 4. Сколько существует точек C таких, что треугольник ABC прямоугольный и его площадь равна 1?
(А) 2
(Б) 4
(В) 6
(Г) 8
(Д) 10
Задача 22.
Какое наименьшее целое значение может принимать выражение $\displaystyle \frac{K⋅A⋅N⋅G⋅A⋅R⋅O⋅O}{G⋅A⋅M⋅E}$‚ если разными буквами обозначены различные ненулевые цифры, а одинаковыми буквами — одинаковые цифры?
(А) 1
(Б) 2
(В) 3
(Г) 5
(Д) 7
Задача 23.
Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлении с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Третий обгон произошёл через 1 час после начала движения. Через сколько минут после третьего случится четвёртый обгон?
(А) 6
(Б) 12
(В) 15
(Г) 20
(Д) 24
Задача 24.
Каждый угол k-угольника равен 90° или 150°. Чему может быть равно k ?
(А) 5
(Б) 8
(В) 9
(Г) 13
(Д) 14
Задача 25.
Дрозды Алекс, Макс и Оскар построили гнезда. Алекс сказал: «От Макса я более чем в два раза дальше, чем от Оскара». Макс сказал: «От Оскара я более чем в два раза дальше, чем от Алекса». Оскар сказал: «От Макса я более чем в два раза дальше, чем от Алекса». Двое из них точно сказали правду. Кто ошибся?
(А) Макс
(Б) Алекс
(В) Оскар
(Г) никто
(Д) невозможно определить
Задача 26.
На листе бумаги изображены четыре прямые l1, l2, l3 и l4. Вася добавил к рисунку оси координат и вычислил угловые коэффициенты этих прямых: k1, k2, k3 и k4 соответственно. Какое из неравенств точно не будет выполняться?
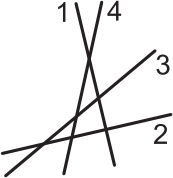
(А) k1 < k2 < k3 < k4
(Б) k4 < k1 < k2 < k3
(В) k3 < k4 < k1 < k2
(Г) k2 < k3 < k4 < k1
(Д) k2 < k4 < k3 < k1
Задача 27.
Требуется вписать числа 1, 2, 3, 4, 6, Зи 9 в кружки так, чтобы произведения чисел на каждой из трёх линий были одинаковыми. Какое число окажется в закрашенном кружке?
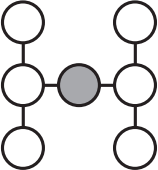
(А) 1
(Б) 2
(В) 6
(Г) 8
(Д) 9
Задача 28.
В треугольнике ABC сумма сторон AB и AC равна 10, а угол BAC равен 30°. Из вершины A проведены высота h, биссектриса l и медиана m. Какое из утверждений А-Г может быть неверным?
(А) h < 5
(Б) m < 5
(В) периметр треугольника не больше 20
(Г) l > 0,5
(Д) все утверждения А-Г обязательно выполняются
Задача 29.
Сейчас произведение возрастов черепах Чапы и Паши равно 23 ⋅ 33 ⋅ 11. Через год произведение их возрастов наверняка не будет делиться на
(А) 7
(Б) 15
(В) 18
(Г) 22
(Д) 55
Задача 30.
На стороне BC треугольника ABC выбрана точка D, а на отрезке AD выбрана точка E. Какую наибольшую величину может иметь наименьший из углов, отмеченных цифрами 1, 2, ..., 9?
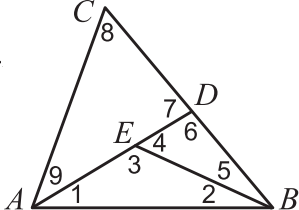
(А) 15°
(Б) 24°
(В) 30°
(Г) 36°
(Д) 45°

