Задача 1.
Какое из слов не имеет ни одной общей буквы со словом КЕНГУРУ?
(А) РОМБ
(Б) УГОЛ
(В) ДИАГОНАЛЬ
(Г) ВЫСОТА
(Д) ВЕРШИНА
Задача 2.
Чему равно 1313,13 : 13?
(А) 11,1
(Б) 101,1
(В) 1010,1
(Г) 101,01
(Д) 11,01
Задача 3.
Сколько минут проходит от середины первой половины часа до конца его второй трети?
(А) 15
(Б) 20
(В) 25
(Г) 30
(Д) 45
Задача 4.
Чему равен квадрат суммы кубов цифр числа 2013?
(А) 64
(Б) 66
(В) 4 ⋅ 62
(Г) 9 ⋅ 62
(Д) 143
Задача 5.
Угол между биссектрисами AD и BD треугольника ABC в пять раза больше угла при вершине C. Чему равен угол при вершине C?
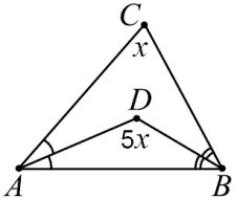
(А) 10°
(Б) 20°
(В) 25°
(Г) 30°
(Д) 35°
Задача 6.
Маша придумала новую операцию с числами: a ∗ b = 2a + 3b. Чему равно 3 ∗ (4 ∗ 5) ?
(А) 51
(Б) 53
(В) 55
(Г) 72
(Д) 75
Задача 7.
Чему может быть равно среднее количество котят у пяти кошек?
(А) 3,3
(Б) 4,2
(В) 4,5
(Г) 4,75
(Д) 5,7
Задача 8.
Каждые восемь минут Алекс зажигает одну свечку. Каждая свечка горит ровно 35 минут, а затем гаснет. Сколько свечек будет гореть через час после того, как Алекс зажёг первую свечку?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 9.
Положительные числа a, b и c таковы, что a3 = b4 и b2 = c3. Тогда
(А) a = c2
(Б) a2 = c3
(В) a2 = c
(Г) a3 = c2
(Д) a = c
Задача 10.
Куб 3 × 3 × 3 покрашен краской. Коля вырезал четыре кубика 1 × 1 × 1 (см. рисунок) и после этого сделал на бумаге отпечатки всех покрашенных граней. Какой картинки у него не получилось?
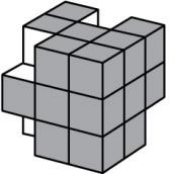
(А) 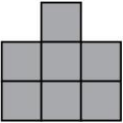
(Б) 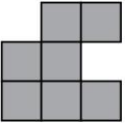
(В) 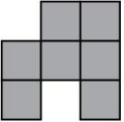
(Г) 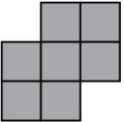
(Д) 
Задача 11.
Периметр трапеции равен 5, и все её стороны — целые числа. Чему равна сумма углов при бóльшем основании этой трапеции?
(А) 60°
(Б) 90°
(В) 105°
(Г) 120°
(Д) 180°
Задача 12.
Марк и Лиза стартуют одновременно из диаметрально противоположных точек круговой аллеи и бегут по этой аллее в одном направлении. Скорость Марка в 9/8 раза больше скорости Лизы. Сколько полных кругов пробежит Лиза, когда Марк догонит её в первый раз?
(А) 2
(Б) 4
(В) 8
(Г) 9
(Д) 17
Задача 13.
Прямоугольник ABCD лежит в I четверти. Его стороны параллельны осям координат (см. рисунок). Для какой из его вершин отношение её ординаты к её абсциссе является наименьшим?
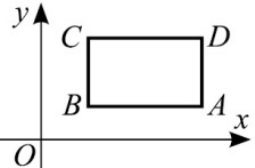
(А) A
(Б) B
(В) C
(Г) D
(Д) ответ зависит от размеров прямоугольника
Задача 14.
У Васи есть 9 чёрных и 18 белых кубиков одинакового размера. Из них он хочет сложить куб 3 × 3 × 3 . Какое наибольшее количество граней чёрных кубиков может оказаться на поверхности получившегося куба?
(А) 27
(Б) 26
(В) 25
(Г) 24
(Д) 18
Задача 15.
На боковой стороне ВС равнобедренного треугольника ABС с основанием AС отмечены точки K и M так, что AM = MK (см. рисунок). Оказалось, что ∠CAM = ∠KAB. Чему равен угол BAM ?
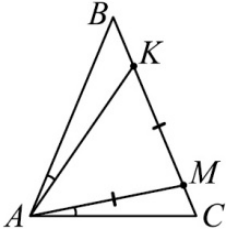
(А) 30°
(Б) 45°
(В) 60°
(Г) 75°
(Д) невозможно определить
Задача 16.
В наборе натуральных чисел 1, 2, …, N не менее 13 чисел делится на 4 и не более 9 чисел делится на 6. Сколько из этих чисел делится на 12?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 17.
Вася выписал несколько последовательных натуральных чисел. Чему не может быть равен процент нечётных чисел среди них?
(А) 60
(Б) 50
(В) 48
(Г) 45
(Д) 40
Задача 18.
На рисунке изображены пять лучей с общим началом. Углы между соседними лучами известны (см. рисунок). Сколько различных лучей окажется на картинке, если провести биссектрисы всех имеющихся углов?
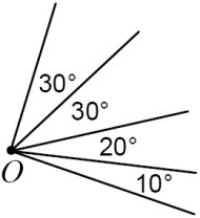
(А) 9
(Б) 11
(В) 12
(Г) 13
(Д) 15
Задача 19.
Все четырёхзначные числа, каждое из которых составлено из четырёх цифр 2, 0, 1, 3, выписали в порядке возрастания. Чему равна наибольшая разность между соседними числами в этой последовательности?
(А) 793
(Б) 703
(В) 702
(Г) 693
(Д) 198
Задача 20.
Петя написал на доске 10 целых чисел. Затем он нашёл произведение каждой пары чисел, написанных на доске. Ровно 15 из этих произведений оказались отрицательными. Сколько нулей среди 10 написанных на доске чисел?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 21.
Джон задумал пятизначное число. Вычеркнув из него одну цифру, он сложил полученное четырёхзначное число с исходным пятизначным числом. Сумма оказалась равна 52713. Чему равна сумма цифр задуманного Джоном пятизначного числа?
(А) 26
(Б) 23
(В) 20
(Г) 19
(Д) 17
Задача 22.
В каждой вершине и на каждом ребре тетраэдра написано одно из десяти чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 11 (каждое число использовано ровно один раз). Число, написанное на ребре, равно сумме чисел, написанных в его концах. На ребре АВ написано число 9 (см. рисунок). Какое число написано на ребре CD?
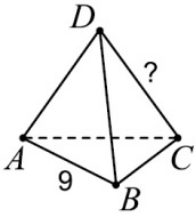
(А) 4
(Б) 5
(В) 6
(Г) 8
(Д) невозможно определить
Задача 23.
На стене висят двое часов. Одни показывают точное время, а другие спешат. Сейчас угол между часовыми стрелками этих часов равен 42°. Чему равен угол между минутными стрелками этих часов?
(А) 144°
(Б) 120°
(В) 84°
(Г) 21°
(Д) 7°
Задача 24.
Федя шифрует натуральные числа. Сначала он выписывает произведение первых двух цифр имеющегося у него числа, за ним произведение второй и третьей цифр, и так далее. Какое число не может получиться у Феди?
(А) 634
(Б) 6454
(В) 3283
(Г) 2012
(Д) 63020
Задача 25.
Пусть S — число точных квадратов, а Q — число точных кубов среди целых чисел от 1 до 20136. Тогда
(А) Q = 2013S
(Б) 2S = 3Q
(В) 3S = 2Q
(Г) S3 = Q2
(Д) S = 2013Q
Задача 26.
Если натуральное число N меньше суммы трёх его наибольших натуральных делителей (исключая само число N), то обязательно
(А) N делится на 4
(Б) N делится на 5
(В) N делится на 6
(Г) N делится на 7
(Д) таких N не существует
Задача 27.
На ветке баобаба сидели 2013 попугаев и разговаривали. Первый попугай сказал: «Второй попугай зелёный». Второй попугай сказал «Третий попугай зелёный», и так далее. 2011-ый попугай сказал: «2012-ый попугай зелёный». Однако 2012-ый попугай сказал: «2013-ый попугай — синий бегемот». На что 2013-ый попугай ответил: «Я не синий бегемот!». Известно, что соврали все зелёные попугаи, и только они. Сколько всего зелёных попугаев сидело на ветке?
(А) 1
(Б) 1006
(В) 1007
(Г) 2012
(Д) 2013
Задача 28.
Сторона квадрата ABCD равна 2013. На стороне AB отмечена точка E так, что AE = 1, а на продолжении стороны AD отмечена точка F так, что ∠AFE = ∠ACE (см. рисунок). Чему равна длина отрезка AF?
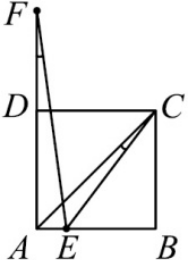
(А) 2013
(Б) 2014
(В) 4024
(Г) 4025
(Д) 6093
Задача 29.
Буратино расставляет по кругу целые числа от 1 до 100. За каждое число, которое больше суммы своих соседей, папа Карло даёт Буратино один золотой. Какое наибольшее количество золотых сможет получить Буратино?
(А) 99
(Б) 50
(В) 49
(Г) 25
(Д) 1
Задача 30.
Какое наибольшее произведение можно получить, если перемножить несколько натуральных чисел, сумма которых равна 2013?
(А) 21006
(Б) 21005 ⋅ 3
(В) 18311
(Г) 11183
(Д) 3671

