Задача 1.
В 2014 году конкурс «Кенгуру» проводится 20 марта. Какой по счёту это день с начала года?
(А) 77
(Б) 78
(В) 79
(Г) 80
(Д) 81
Задача 2.
Арина разбирает мамины бусы. Она хочет снять 5 тёмных бусин. Какое наименьшее количество белых бусин ей потребуется снять для этого?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 3.
Какое слово написано верно?
(А) перимитр
(Б) пириметр
(В) периметор
(Г) приметр
(Д) периметр
Задача 4.
Два кольца, белое и тёмное, зацеплены друг за друга так, как изображено на рисунке справа. Как эти кольца выглядят с другой стороны?
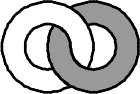
(А) 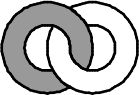
(Б) 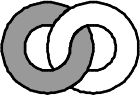
(В) 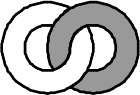
(Г) 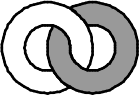
(Д) 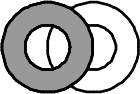
Задача 5.
Торт весит 900 г. Павел разрезал его на несколько частей так, что самая большая часть весит столько же, сколько весят вместе все остальные части. Сколько весит бóльшая часть?
(А) 100 г
(Б) 200 г
(В) 300 г
(Г) 450 г
(Д) 600 г
Задача 6.
В примере ниже три цифры заменили звёздочками. Какова сумма этих цифр?

(А) 0
(Б) 9
(В) 10
(Г) 11
(Д) 19
Задача 7.
Вася выписал на доске все целые числа от 1 до 100, а Веня вычел каждое из них из числа 133 и выписал результаты. Сколько чисел написано дважды?
(А) 64
(Б) 65
(В) 66
(Г) 67
(Д) 68
Задача 8.
Электронные часы Бена идут правильно, но горизонтальные линии самой правой цифры не загораются. Полминуты назад часы показывали то, что изображено на рисунке 1. Сейчас они показывают то, что изображено на рисунке 2. Сколько сейчас времени?
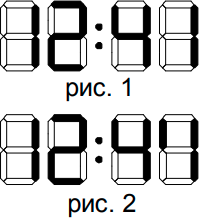
(А) 12:40
(Б) 12:42
(В) 12:44
(Г) 12:47
(Д) 12:49
Задача 9.
Какой квадратик надо добавить, чтобы в получившемся квадрате была закрашена ровно половина площади?

(А) 
(Б) 
(В) 
(Г) 
(Д) это невозможно
Задача 10.
Произведение цифр трёхзначного числа равно 135. Какова сумма цифр этого числа?
(А) 14
(Б) 15
(В) 16
(Г) 17
(Д) 18
Задача 11.
Выбрав четыре из пяти деталей А-Д, можно составить квадрат. Какая деталь не будет использована?
(А) 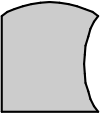
(Б) 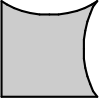
(В) 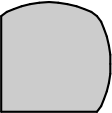
(Г) 
(Д) 
Задача 12.
Доктор Пилюлькин прописал семи коротышкам по одной пилюле каждый день, а девяти другим коротышкам — по одной пилюле через день. Сегодня доктор Пилюлькин выдал этим коротышкам 13 пилюль. Сколько пилюль он выдаст им завтра?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 13
Задача 13.
На рисунке AF = 35, AC = 12, BD = 11, CE = 12, DF = 16. Чему равна длина отрезка BE?
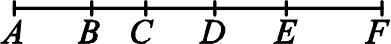
(А) 17
(Б) 16
(В) 15
(Г) 14
(Д) 13
Задача 14.
Какое наибольшее число можно получить, если из разности двух трёхзначных чисел вычесть сумму трёх различных двузначных чисел?
(А) 865
(Б) 866
(В) 867
(Г) 869
(Д) 870
Задача 15.
Саша принесла с пляжа ракушки. Когда она попыталась разделить их на 3 равные кучки, осталось 2 ракушки. Тогда она попыталась поделить все эти ракушки на 5 равных кучек, но опять осталось 2 ракушки. Какое наименьшее количество ракушек надо добавить, чтобы все ракушки можно было разложить поровну и на 3 кучки, и на 5 кучек?
(А) 2
(Б) 3
(В) 8
(Г) 13
(Д) 14
Задача 16.
Какой кубик получится из данной развёртки?
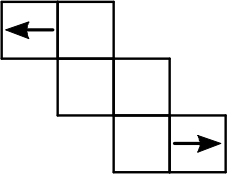
(А) 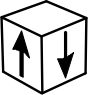
(Б) 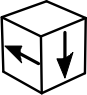
(В) 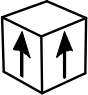
(Г) 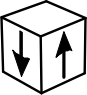
(Д) 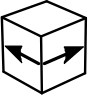
Задача 17.
В 12:00 Петя пошёл в соседнюю деревню. Вместе с ним в том же направлении выбежал пёс Шарик. Добежав до соседней деревни в 14:30, Шарик повернул обратно и встретил Петю в 15:30. Во сколько раз скорость Шарика больше скорости Пети?
(А) 4/3
(Б) 3/2
(В) 2
(Г) 5/2
(Д) 7/3
Задача 18.
Число 111…111 (2014 единиц) умножили на 101. Какова сумма цифр произведения?
(А) 2014
(Б) 2016
(В) 4026
(Г) 4027
(Д) 4028
Задача 19.
После того, как в 3 часа ночи прозвенел Васин будильник, и Вася стукнул по нему кулаком, часовая стрелка будильника стала двигаться в 12 раз быстрее, чем надо. Что покажет будильник в 03:55?
Комментарий: скорость минутной стрелки не изменилась.
(А) 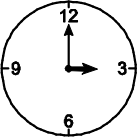
(Б) 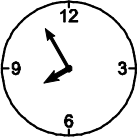
(В) 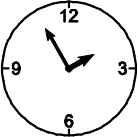
(Г) 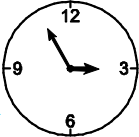
(Д) 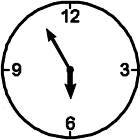
Задача 20.
На доске написаны целые числа от 1 до 10. Петя хочет стереть несколько из них так, чтобы произведение оставшихся не делилось на 6. Какое наименьшее количество чисел ему придётся стереть?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 21.
Через два часа до сегодняшней полуночи останется втрое больше времени, чем 6 часов назад оставалось до полудня. Через сколько часов наступит полночь?
(А) 2
(Б) 4
(В) 6
(Г) 8
(Д) 10
Задача 22.
Куб 3 × 3 × 3 сделан из 27 маленьких кубиков. Какое наименьшее количество кубиков нужно вынуть, чтобы вид спереди, сверху и справа был таким, как на рисунке?
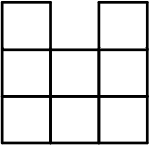
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 9
Задача 23.
Кролик Эдуард в день съедает либо 9 морковок, либо 2 кочана капусты, либо 1 кочан капусты и 4 морковки, но в некоторые дни он ест только траву. За 10 дней Эдуард съел 30 морковок и 9 кочанов капусты. Сколько из этих дней он питался только травой?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 24.
В Волшебной стране каждому дождливому дню обязательно предшествуют три солнечных дня, а через неделю после каждого солнечного дня снова наступает солнечный день. На какое наибольшее число дней вперёд можно предсказать погоду в дождливый день?
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 8
Задача 25.
Сандра бегает в два раза быстрее, чем Бренда, а Бренда — в два раза быстрее, чем Николь. Девочки одновременно стартовали из одной точки кольцевой дорожки: Сандра побежала в одну сторону, а Бренда и Николь — в другую. Сначала Сандра встретила Бренду, а через 200 метров — Николь. Чему равна длина дорожки?
(А) 800 м
(Б) 1000 м
(В) 1500 м
(Г) 2000 м
(Д) невозможно определить
Задача 26.
Пусть N — наименьшее натуральное число, остатки от деления которого на 2, 3, 4, 5 и 6 различны. Какой остаток оно даёт при делении на 5?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 27.
Числа 1, …, 9 вписали в 9 клеток и выполнили действия, указанные в каждой строчке и каждом столбце. Результаты действий записали в кружках (см. рисунок). Какое число написано в клетке, отмеченной звёздочкой?
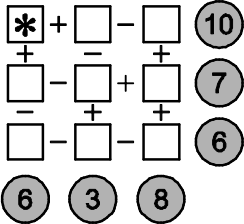
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 28.
На острове живут 25 человек: рыцари, которые всегда говорят правду, лжецы, которые всегда лгут, и хитрецы, каждый из которых через раз отвечает на вопросы то правду, то ложь. Каждому жителю острова было задано подряд три вопроса: «Вы рыцарь?», «Вы хитрец?», «Вы лжец?». Ответ «Да» на первый вопрос дали 17 человек, на второй — 12, на третий — 8. Сколько хитрецов на острове?
(А) 4
(Б) 5
(В) 8
(Г) 16
(Д) невозможно определить
Задача 29.
На какое из чисел А-Д могут различаться суммы цифр двух последовательных целых чисел?
(А) 2011
(Б) 2012
(В) 2013
(Г) 2014
(Д) 2015
Задача 30.
На столе стоит 30 тарелок, на каждой из которых лежит не более 30 булочек. Время от времени в окно влетает Карлсон, выбирает несколько тарелок и съедает одинаковое количество булочек с каждой из них. За какое наименьшее число визитов Карлсон наверняка сможет съесть все булочки?
(А) 4
(Б) 5
(В) 6
(Г) 15
(Д) 30

