Задача 1.
Какой буквы из слова КЕНГА нет на рисунке?
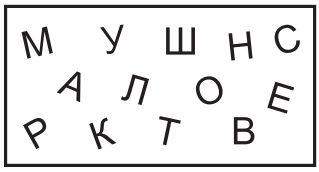
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) А
Задача 2.
Крошка Ру сегодня отмечает 1 год и 3 месяца. Через сколько месяцев ему будет 2 года?
(А) 3
(Б) 5
(В) 7
(Г) 8
(Д) 9
Задача 3.
Сколько верёвочек изображено на рисунке?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 4.
В Тридевятом царстве погода меняется каждый день: день идёт дождь, день светит солнце. Сколько солнечных дней будет в неделе, которая началась дождливым понедельником?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 5.
В какую из точек лабиринта можно попасть из точки О?
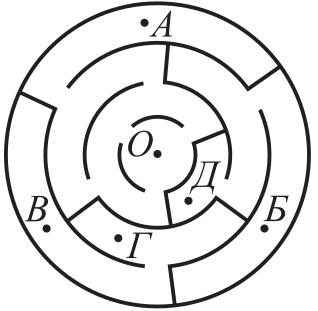
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 6.
Ближайший год, в записи которого будут те же 4 цифры, что и в 2016 году, — это
(А) 1206
(Б) 2106
(В) 2601
(Г) 2061
(Д) 2026
Задача 7.
У подъезда висит табличка (см. рисунок). На каком этаже находится квартира с номером 27?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 8.
В каком из этих чисел цифра десятков в два раза больше, чем цифра единиц?
(А) 124
(Б) 424
(В) 753
(Г) 263
(Д) 135
Задача 9.
Два кенгурёнка Кузя и Пузя прыгают по клеточкам навстречу друг другу (см. рисунок). Они прыгают одновременно, но Кузя прыгает на соседнюю клеточку, а Пузя — через одну клеточку. На какой клеточке они встретятся?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 10.
По разные стороны дорожки стоят таблички с буквами (см. рисунок). Маша прошла по этой дорожке из точки 1 в точку 2 и прочитала только то, что видела справа от себя. Что у неё получилось?
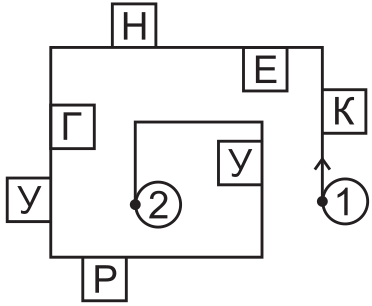
(А) КГРУ
(Б) КЕНР
(В) КНУ
(Г) КНГР
(Д) КНУР
Задача 11.
Если из самого большого двузначного числа вычесть самое маленькое двузначное число, то получится
(А) 88
(Б) 89
(В) 90
(Г) 91
(Д) 99
Задача 12.
Четыре карточки, изображённые ниже, уложили в квадратную коробку с белым дном. Что могло получиться?
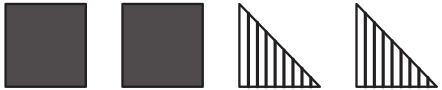
(А)
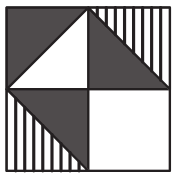
(Б)
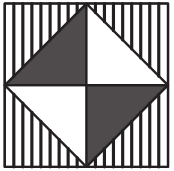
(В)
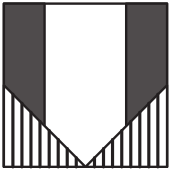
(Г)
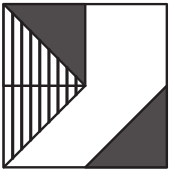
(Д)
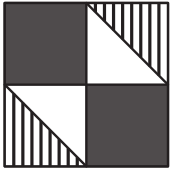
Задача 13.
Сколько времени остаётся до полуночи, если сейчас половина девятого вечера?
(А) 210 минут
(Б) 180 минут
(В) 150 минут
(Г) 120 минут
(Д) 90 минут
Задача 14.
В доме 12 комнат, и в каждой комнате по два окна. Вечером был виден свет в 18 окнах. В скольких комнатах свет не был включён?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 15.
Женя сначала нарисовала 4 маленьких квадратика (см. рисунок). Потом она пририсовала к ним ещё несколько таких же квадратиков так, что получился большой квадрат. Сколько квадратиков она могла дорисовать?
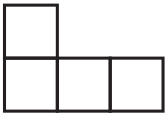
(А) 2
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 16.
Сумма двух идущих подряд чисел равна 21. Чему равно их произведение?
(А) 22
(Б) 80
(В) 90
(Г) 100
(Д) 110
Задача 17.
У ребристого колючего кактуса 8 рёбер, и на каждом ребре растёт по 6 или по 7 колючек (см. рисунок). Рёбра с шестью и с семью колючками чередуются. Сколько колючек не видно на рисунке?
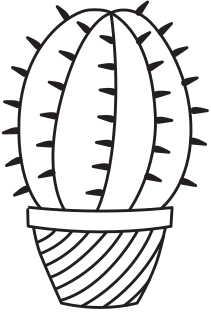
(А) 18
(Б) 19
(В) 20
(Г) 21
(Д) 26
Задача 18.
Оля уехала в лагерь на 25 дней. По воскресениям к ней приезжала мама. Какое самое большое число раз мама могла к ней приезжать?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 19.
Маленький гном забыл код замка от двери в свою пещеру. Он помнит, что код состоит из четырёх цифр 1, 2, 3, 4, и уже попробовал 4 варианта: 3421, 4123, 3214, 2134, но все они не подошли. Найдите правильный код, если известно, что каждую цифру гном поставил на нужное место два раза.
(А) 4321
(Б) 3124
(В) 3142
(Г) 2143
(Д) 1324
Задача 20.
Карточку, изображённую ниже, перевернули сначала через левый край, а потом — через верхний край. Что получилось?
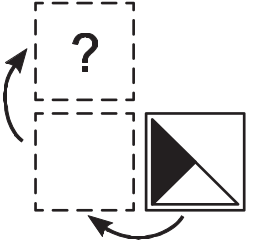
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 21.
Джон нарисовал полоску из 11 клеток и укладывает 8 монет по одной в клетку так, чтобы между монетами не было пустых клеток. Это можно сделать разными способами, но есть клетки, в которых при любом способе будет лежать монета. Сколько таких клеток?

(А) 1
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 22.
Бабушка раздала 10 пирожков своим пяти внукам. Каждому досталось не меньше одного пирожка. Что может быть верно?
(А) Кто-то получил 6 пирожков, а кто-то – 2.
(Б) Три внука получили по 3 пирожка.
(В) Два внука получили по 4 пирожка.
(Г) Четыре внука получили по одному пирожку.
(Д) Ровно четыре внука получили по 2 пирожка.
Задача 23.
На четырёх из рисунков А-Д нарисован один и тот же барабан, а на одном — другой. На каком?
(А)
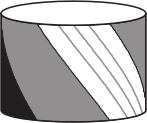
(Б)
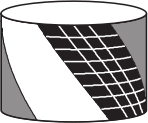
(В)
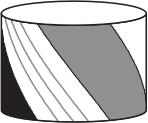
(Г)
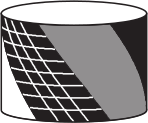
(Д)
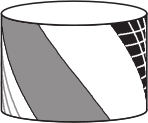
Задача 24.
Дату записывают восемью цифрами. Например, 25.06.1987 — 25 июня 1987 года. Заметим, что в записи этой даты ни одна цифра не повторяется дважды. Какими будут первые две цифры в записи следующей даты с таким же свойством?
(А) 08
(Б) 12
(В) 17
(Г) 23
(Д) 25
Задача 25.
В числовом ребусе ГНОМ + ГНОМ = СКАЛА разные буквы обозначают разные цифры. Какую цифру обозначает буква Г, если М = 3?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9

