Будильник равномерно отстает на 4 минуты в час. Три с половиной часа тому назад он был поставлен точно. Сейчас на часах, показывающих точное время, 12 часов. Через сколько минут (точного времени) на будильнике тоже будет 12 часов?

Сколько есть двузначных чисел, у которых цифра десятков отличается от цифры единиц более чем на 2?

В каждой ячейке таблицы 3 × 3 записано некоторое число, причём в каждой ячейке, в которой есть соседняя ячейка слева, записанное число, вдвое больше того, которое записано в соседней ячейке слева, а в каждой ячейке, в которой есть соседняя ячейка сверху, записанное число, втрое больше того, которое записано в соседней ячейке сверху. Известно, что сумма всех девяти чисел равна 182. Какое число записано в центральной ячейке таблицы?

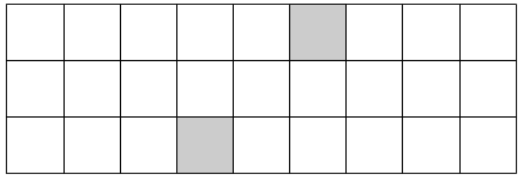
Из прямоугольника 3 × 9 вырезали две клетки. Разрежьте полученную фигуру на три части и сложите из них квадрат.

На доске написано число 27. Каждую минуту число стирают с доски и записывают на его место произведение его цифр, увеличенное на 12. Например, через минуту на доске будет написано число 2 ⋅ 7 + 12 = 26. А что окажется на доске через час?

На острове живут 200 аборигенов: 100 рыцарей, которые говорят исключительно правду, и 100 лжецов, которые всегда лгут. У каждого из жителей острова есть хотя бы один друг. Как-то 100 жителей острова одновременно сказали: «Каждый мой друг — рыцарь». В этот же момент остальные 100 жителей сказали: «Каждый мой друг — лжец». Какое наименьшее количество пар, состоящих из рыцаря и лжеца, которые дружат между собой, может быть на острове? Один и тот же абориген может входить в несколько разных пар.