Задача 1.
Можно ли из данных двух кусочков проволоки сложить фигуру имеющую ось симметрии? Фигуры можно поворачивать и переворачивать.
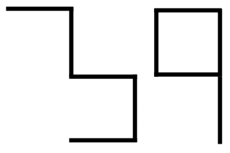
Задача 2.
У Лилианы и Тимура было по прямоугольному листу бумаги одинаковых размеров. Каждый из них разрезал свой лист на две части и получил два новых прямоугольника. Лилиана посчитала периметры своих прямоугольников и сложила результаты. Получилось 18 см. Тимур произвёл такие же расчёты со своими прямоугольниками и получил 24 см. Чему равен периметр исходного листа бумаги?
Задача 3.
Девять школьников из пяти городов добирались на Турнир Мёбиуса на поезде. Каждый из них ночью упал с полки, кто-то несколько раз. Утром выяснилось, что произошло 19 падений. Причём школьники из одного города падали одинаковое количество раз, а из разных городов — разное. Афанасий из Москвы упал два раза. Сколько ещё школьников падало с полки два раза?
Задача 4.
На Турнир Мёбиуса приехало 64 школьника, их расселили по 13 комнатам и на двери каждой комнаты написали количество школьников, которые в ней проживают. Может ли произведение этих чисел быть нечётным числом?
Задача 5.
Алёна сложила из одного комплекта домино фигуру. На рисунке показано только как расположились половинки доминошек. Покажите, как располагались доминошки. Объясните, почему они располагаются именно так.
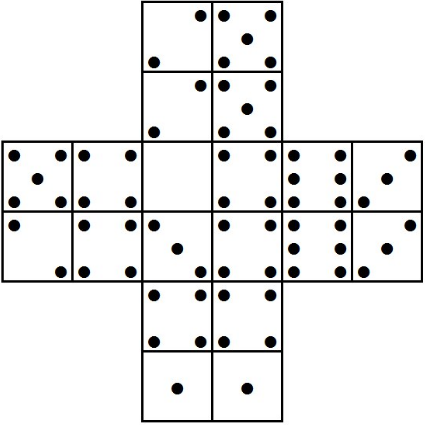
Задача 6.
У слесаря Ангелины есть набор редукторов которые могут изменить скорость в 2, 3, 5 и 7 раз. Можно ли увеличить скорость вращения в 2018 раз?

