Замените в выражении $(x^4 - 3)^2 + (x^3 + ∗)^2$ звёздочку на одночлен так, чтобы после возведения в квадрат и приведения подобных слагаемых получилось четыре слагаемых.

Каково отношение площади закрашенной части к белой (вершины всех квадратов за исключением самого большого находятся в серединах соответствующих сторон)?

Назовём число зеркальным, если слева направо оно «читается» так же, как справа налево. Например, число 12321 — зеркальное.

1. Напишите какое-нибудь зеркальное пятизначное число, которое делится на 5.
2. Сколько существует пятизначных зеркальных чисел, которые делятся на 5?

Вася задумал два числа (необязательно целые). Их сумма равна их произведению и равна их частному. Какие числа задумал Вася?

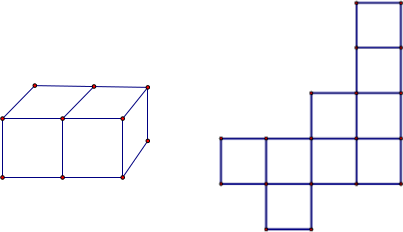
Петя разрезал бумажный параллелепипед 2×1 по его рёбрам и получил развёртку. Потом Дима отрезал один квадратик от этой развёртки, и осталось девять квадратиков, как на рисунке. Где мог быть отрезанный квадратик? Нарисуйте полную развёртку и отметьте на ней отрезанный квадратик. (Достаточно привести один правильный вариант развёртки).

Каждый из 10 гномов либо всегда говорит правду, либо всегда лжёт. Известно, что каждый из них любит ровно один сорт мороженого: сливочное, шоколадное или фруктовое. Сначала Белоснежка попросила поднять руки тех, кто любит сливочное мороженое, и все подняли руки, потом тех, кто любит шоколадное мороженое — и половина гномов подняли руки, потом тех, кто любит фруктовое мороженое — и руку поднял только один гном. Сколько среди гномов правдивых?