В зимней математической школе начальник смены повел школьников кататься на лыжах. Начало и конец маршрута – в точке С (см. рисунок).

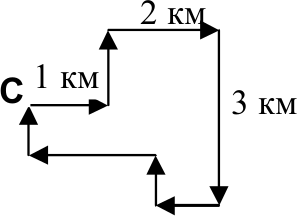
Могли ли школьники пройти 10 километров по этому маршруту?

Аня, Саша и Витя и Настя решали контрольную, на которой задали 9 задач. Могло ли быть так, что Аня списала семь задач у Саши, Саша списал семь задач у Вити, Витя списал семь задач у Насти, а Настя списала семь задач у Ани?

Юля, Семён, Василиса, Илларион и Татьяна Петровна ели конфеты (причём, не деля их на части). Когда все конфеты кончились, их спросили: «Кто сколько съел конфет?» На что они ответили:

• Юля: «Я и Василиса съели 97 конфеты»;
• Семён: «Я и Илларион съели 234 конфеты»;
• Василиса: «Я, Семён и Татьяна Петровна съели 153 конфет»;
• Илларион: «Я, Татьяна Петровна и Юля съели 277 конфет».

После этого Татьяна Петровна сказала, что так быть не могло. Почему она пришла к такому выводу?

У Буратино есть 6 монет: две золотые, две серебряные и две медные. В каждой паре одна монета настоящая, а другая фальшивая. Известно, что все настоящие монеты весят одинаково и все фальшивые тоже весят одинаково. Как за 2 взвешивания на чашечных весах без гирь найти все настоящие монеты?

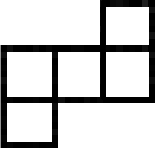
Клетки тетрадного листа раскрашены в 8 цветов. Докажите, что найдётся фигура вида, как на рисунке, внутри которой есть две клетки одного цвета.