Задача 1.
Толя задумал число. Сначала он прибавил к нему 1, потом полученную сумму умножил на 2, а затем отнял 5. Получилось 17. Какое число он задумал?
Задача 2.
Если Петя отдаст половину своих конфет Маше, то у Маши станет на 5 конфет больше, чем у Пети. Сколько у Маши конфет сейчас?
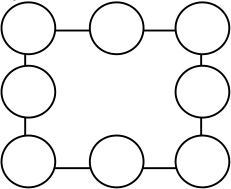
Задача 3.
Расставьте числа 2,6,0,1,2,0,1,4 в вершинах и серединах сторон квадрата так, чтобы суммы чисел, стоящих на каждой из сторон, делились на 3.
Задача 4.
Лесоруб Петрович распиливает четыре 5-метровых бревна на метровые чурбаки за 20 мин, а лесоруб Палыч за это время распиливает на метровые чурбаки семь 3-метровых брёвен. Кто из них быстрее распилит 10-метровое бревно на чурбаки?
Задача 5.
В ящике лежат шарики (не меньше 7) нескольких цветов. Если вытащить любые пять шариков, то среди них обязательно найдутся два шарика одного цвета. А если вытащить любые семь, то обязательно найдутся два шарика разных цветов. Какое максимальное число шариков может быть в коробке? А минимальное?
Задача 6.
Федя каждый день ест одинаковое количество витаминок. Витаминки продаются в большой, средней или маленькой упаковке. В большой витаминок в три раза больше, чем в маленькой, а в средней в два раза больше, чем в маленькой. Большая упаковка у Феди полностью заканчивается ровно за 50 дней. Маленькой упаковки хватает только на 16 дней, но в ней после этого ещё остаётся несколько витаминок. На сколько дней хватит средней упаковки?
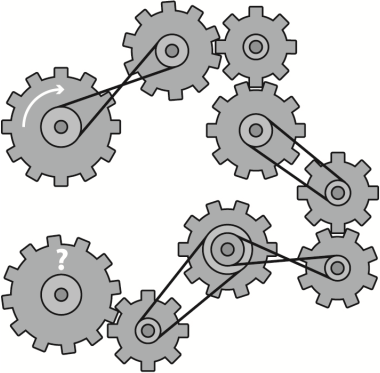
Задача 7.
На рисунке шестерёнки сцеплены друг с другом зубцами или ремнями. Укажите на рисунке, в какую сторону будет крутиться последняя шестерёнка.
Задача 8.
В приведённом ниже выражении поставьте два знака арифметических действий («+», «–», «×» или «÷», можно одинаковые), чтобы значение выражения было наибольшим. Число не может начинаться с нуля.
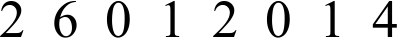
Задача 9.
Встретились три человека, каждый из которых либо всегда говорит правду, либо всегда лжёт. Первый сказал: «Среди нас один лжец», второй: «Среди нас два лжеца», третий: «Среди нас три лжеца». Кто есть кто?
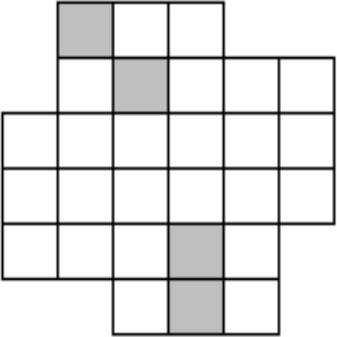
Задача 10.
Разрежьте приведённую фигуру по линиям сетки на четыре одинаковые части так, чтобы в каждой части было ровно по одной закрашенной клетке.