Задача 1.
Запишите наименьшее пятизначное число, делящееся на 3, все цифры которого различны.
Задача 2.
В приведённом ниже выражении поставьте знаки арифметических действий («+», «–», «×» или «÷», можно одинаковые) и один знак равенства, чтобы получилось верное равенство.
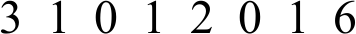
Задача 3.
У квадратного листа бумаги загнули один угол так, что вершина оказалась в центре квадрата (см. рисунок).
Площадь получившегося пятиугольника на 2 см2 меньше площади исходного квадрата. Чему равна сторона квадрата?
Задача 4.
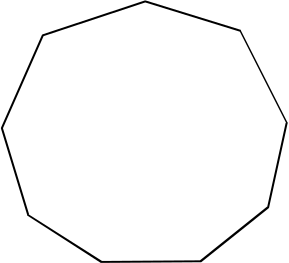
Разрежьте правильный 9-угольник ровно на 7 равнобедренных треугольников.
Задача 5.
В 5Ю классе 7 человек едят мороженое каждый день, 9 человек едят мороженое через день, а остальные не едят мороженого вообще. Вчера 13 учеников этого класса ели мороженое. Сколько учеников будут есть мороженое сегодня?
Задача 6.
Обычно Илья Яковлевич отдыхает только по субботам и воскресеньям. Но в феврале 2010 года Илье Яковлевичу предоставили отпуск длиной 12 дней подряд. Какое максимальное и какое минимальное количество дней непрерывного отдыха могло получиться у Ильи Яковлевича в феврале? (Если суббота или воскресенье попадают в дни отпуска, то они считаются днями отпуска).
Задача 7.
Одиннадцать друзей Оушена, он сам и Терри встали в круг, чтобы считалкой определить, кто будет играть в шахматы. Считает Терри, он начинает с соседа слева и далее по часовой стрелке. Где нужно встать Оушену, чтобы в результате выбыли все кроме него и Терри? Известно, что Терри всегда использует считалку «Вышел-месяц-из-тумана-вынул-ножик-из-кармана».
Задача 8.
Из 4 фигурок, каждая из которых состоит из 4 кубиков, сложили прямоугольный параллелепипед как на рисунке. Каждая фигурка окрашена в свой цвет. Как выглядит белая фигурка?
Задача 9.
Ваня шёл по левой стороне улицы и считал сумму цифр всех номеров домов, что видел на этой стороне. В некоторый момент (когда он прошёл не менее двух домов) у него получилось 51. В этот момент он остановился и на другой стороне улицы увидел номер 17. У какого максимального количества домов он мог сосчитать сумму? А у какого минимального?
Задача 10.
Мальчики Паша, Коля, Толя и девочки Маша и Света собрались на каток. Но в результате пошли не все. На вопрос, кто же все-таки ходил, ребята ответили так:
- Толя: нас было четверо.
- Маша: мальчиков было больше девочек.
- Паша: нас было трое.
- Света: мы с Машей обе были.
- Коля: Толи не было.
Кто ходил на каток, если правду сказали только те, кто ходил, а остальные солгали? Укажите все возможные варианты.

