Задача 1.
На какую цифру оканчивается произведение всех чисел, делящихся на 2017 и меньших 20170?
Задача 2.
У Егора и Артёма вместе 45 марок. Половина марок Егора равна трети марок Артёма. Сколько марок у каждого мальчика?
Задача 3.
Три одинаковых квадрата приложили друг к другу стороной (без наложений) так, что получился прямоугольник. Чему равна площадь прямоугольника, если его периметр равен 48 см?
Задача 4.
В компании детей среди любых четырёх есть Саша. А среди любых трёх есть девочка. Какое наибольшее количество Александров (мальчиков) может быть в этой компании?
Задача 5.
Петя сложил три последовательных числа и получил число с разными цифрами. Переписывая результат в тетрадь, он забыл дописать последнюю цифру и записал 1046. Какие три числа сложил Петя?
Задача 6.
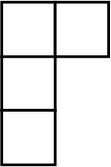
К четырёхклеточной фигуре, имеющей форму буквы Г, требуется добавить ещё одну клетку так, чтобы получилась фигура, имеющая ось симметрии. Сколькими способами это можно сделать?
Задача 7.
Электронные часы показывают время в 24 часовом формате. Какое максимальное число минут подряд на экране будут высвечиваться четыре цифры, идущие в порядке: а) возрастания; б) неубывания?
Комментарий: Вместо 24:00 часы показывают 00:00.
Задача 8.
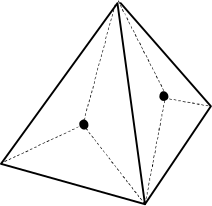
В бумажной пирамидке на каждой грани выбрали точку, соединили её синим отрезком с вершинами граней и разрезали по всем синим отрезкам. Сколько получилось бумажных кусочков?
Задача 9.
Оля, Вася, Маша и Петя – ученики 4, 5, 6 и 7 классов. На вопрос, кто кого старше, ребята сказали:
- Оля: «Маша старше Пети»
- Вася: «Оля младше Пети»
- Маша: «Петя старше Васи»
- Петя: «Маша младше Оли».
Позже выяснилось, что если кто-то высказался про школьника старше его самого, то он соврал. Все остальные утверждения были верными. Определите, кто в каком классе учится.
Задача 10.
Лёша записал на доске натуральное число, меньшее 1000. Каждую секунду он делит текущее число на доске на 2, если оно чётное и записывает результат деления вместо предыдущего числа. Если же число на доске нечётно, он прибавляет к нему 1 и тоже записывает результат сложения вместо прежнего числа. Через какое наибольшее число ходов у Лёши может впервые получиться число 1 на доске?
Например, если было записано 5, то мы получаем 1 через 5 ходов:
5 ⟶ 6 ⟶ 3 ⟶ 4 ⟶ 2 ⟶ 1

