Задача 1.
У некоторой пирамиды 7 граней. Сколько у неё рёбер?
(А) 8
(Б) 9
(В) 12
(Г) 18
(Д) 21
Задача 2.
Вольер для кенгуру в зоопарке имеет форму прямоугольника 40 м х 60 м. На плане зоопарка изображение этого вольера имеет периметр 100 см. В каком масштабе выполнен план?
(А) 1 : 100
(Б) 1 : 150
(В) 1 : 160
(Г) 1 : 170
(Д) 1 : 200
Задача 3.
Если $\displaystyle \frac{x − y}{x + y} = \frac{12}{13}$, то $\displaystyle \frac{x^2}{y^2}$ равно:
(А) $\displaystyle \frac{13}{12}$
(Б) $\displaystyle \frac{25}{6}$
(В) $\displaystyle \frac{144}{169}$
(Г) 25
(Д) 625
Задача 4.
Чему равен угол ADC, если ВС = AD?
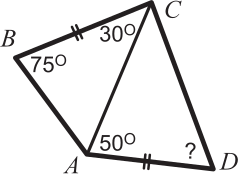
(А) 30º
(Б) 50º
(В) 55º
(Г) 65º
(Д) 70º
Задача 5.
Корень седьмой степени из числа $7^{7^7}$ равен:
(А) $6^{7^7}$
(Б) $7^{6^7}$
(В) $7^{7^6}$
(Г) $7^{7^7-1}$
(Д) $6^{7^6}$
Задача 6.
В клетчатом квадрате 2003 × 2003 закрашены все клетки на обеих диагоналях. Сколько клеток остались незакрашенными?
(А) 20022
(Б) 2002 ⋅ 2001
(В) 2002 ⋅ 2003
(Г) 2001 ⋅ 2003
(Д) 2004 ⋅ 2001
Задача 7.
Какое множество точек задаётся на плоскости уравнением |у| = х2?
(А) 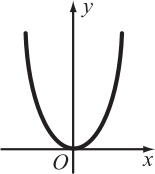
(Б) 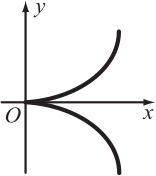
(В) 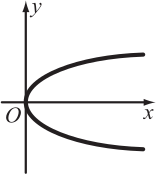
(Г) 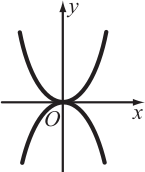
(Д) 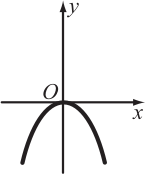
Задача 8.
У скольких двузначных чисел сумма цифр суммы цифр равна 1?
(А) 1
(Б) 2
(В) 9
(Г) 10
(Д) другой ответ
Задача 9.
На какое наименьшее количество четырёхугольников можно разрезать правильный девятиугольник?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) нельзя разрезать
Задача 10.
В корзине лежат 30 грибов — несколько белых и несколько подберёзовиков. Если мы вынем 12 грибов, то среди них обязательно будет хотя бы один белый. Если мы вынем 20 грибов, то среди них обязательно будет хотя бы один подберёзовик. Сколько белых грибов в корзине?
(А) 11
(Б) 12
(В) 19
(Г) 20
(Д) 29
Задача 11.
В аквариуме, площадь основания которого 2 дм2, вода достигала высоты 5 см. Пустую банку с площадью основания 1 дм2 и высотой 7 см погрузили на дно аквариума. Вода в аквариуме поднялась, и часть её перелилась в банку. Какого уровня достигла вода в банке?
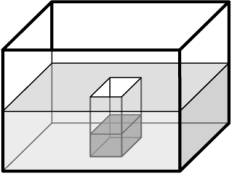
(А) 1 см
(Б) 2 см
(В) 3 см
(Г) 4 см
(Д) 5 см
Задача 12.
Часовая стрелка часов имеет длину 4 см, а минутная — 8 см. Каково отношение расстояний, проходимых концами стрелок от 2 до 5 часов дня?
(А) 1 : 2
(Б) 1 : 4
(В) 1 : 6
(Г) 1 : 12
(Д) 1 : 24
Задача 13.
Петя хочет сделать скамейку в саду из половинок стволов дерева (см. рисунок). Диаметры нижних стволов — 2 дм, верхнего — 4 дм. Какова высота скамейки?
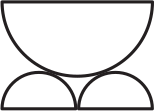
(А) 3 дм
(Б) √8 дм
(В) 2,85 дм
(Г) √10 дм
(Д) 2,5 дм
Задача 14.
Если a и b — числа разных знаков, то самым большим из четырёх чисел q = a2 – b2, r = (a + b)2, s = (a – b)2, t = a2 + b2 является:
(А) q
(Б) r
(В) s
(Г) t
(Д) ответ зависит от чисел a и b
Задача 15.
Ковровая дорожка толщиной 1 см свернута в рулон так, что получился цилиндр диаметра 1 м. Тогда длина дорожки приближенно равна
(А) 20 м
(Б) 50 м
(В) 75 м
(Г) 150 м
(Д) 300 м
Задача 16.
Сколько существует квадратов с вершиной А(−1; 1), для которых хотя бы одна из координатных осей является осью симметрии?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 17.
Сколько среди чисел 1, 2, …, 50 таких, которые равны сумме всех своих простых делителей?
(А) 10
(Б) 15
(В) 17
(Г) 19
(Д) 22
Задача 18.
«Рыбка» состоит из правильного шестиугольника и двух правильных треугольников. Отношение площади «рыбки» к площади заштрихованного треугольника равно:
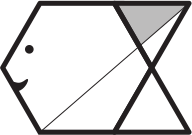
(А) 12
(Б) 8
(В) 10
(Г) 13
(Д) другой ответ
Задача 19.
Закончите фразу так, чтобы получилось неверное утверждение: «Для всякого числа х найдётся такое число у, что …»
(А) х2 + у2 > 100
(Б) у2 − х2 > 100
(В) х2 – у2 > 100
(Г) (х − у)2 > 100
(Д) х3 − у3 > 100
Задача 20.
Площади остроугольного треугольника, квадрата и ромба равны. При этом основание треугольника равно стороне квадрата и равно одной из диагоналей ромба. Тогда для периметров этих фигур выполнены неравенства:
(А) Р□ < Р◊ < Р∆
(Б) Р◊ < Р□ < Р∆
(В) Р∆ < Р◊ < Р□
(Г) Р∆ < Р□ < Р◊
(Д) Р◊ < Р∆ < Р□
Задача 21.
Если a и b — корни уравнения x2 + x − 2004 = 0, то число a2 + 2b2 + ab + b − 2004 равно:
(А) 2004
(Б) 2004,5
(В) 2005
(Г) 2006
(Д) 1002
Задача 22.
Сколько чисел от 1900 до 2000 могут быть записаны в виде 2n − 2k, где n и k — натуральные числа?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 23.
Жан-Кристоф продолжает изучать русский язык. Он выписал (цифрами и словами) все натуральные числа, меньшие миллиона, у которых сумма цифр равна количеству слов, используемых при словесной записи этого числа. Например, для числа 1001 (тысяча один) сумма цифр и количество слов равны двум. Какая самая большая сумма цифр встретилась у выписанных чисел?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 24.
Вычислите: $\displaystyle \left(\frac{1 + 2}{3} + \frac{4 + 5}{6} + \ldots + \frac{2002 + 2003}{2004}\right) + \left(1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{668}\right)$
(А) 668
(Б) 1336
(В) 2002
(Г) 2003
(Д) 2004
Задача 25.
Бутылка заполняется водой, равномерно текущей из крана. График показывает зависимость высоты h воды в бутылке от времени.
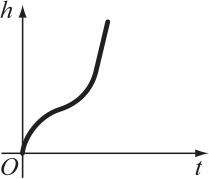
Какой может быть форма бутылки?
(А) 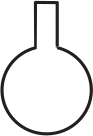
(Б) 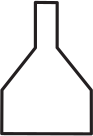
(В) 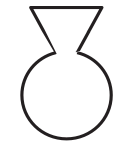
(Г) 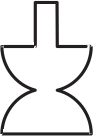
(Д) 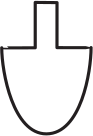
Задача 26.
По листу клетчатой бумаги со стороной клетки 1 см ползёт жук. Он проделал путь длиной 3 см. Каково наибольшее количество клеток, внутри которых мог побывать жук?
(А) 3
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 27.
На боковых гранях куба расставлены натуральные числа, а в каждой вершине написано число, равное произведению чисел на трёх прилегающих к этой вершине гранях. Сумма чисел в вершинах равна 70. Какова сумма чисел на гранях?
(А) 12
(Б) 35
(В) 14
(Г) 10
(Д) невозможно определить
Задача 28.
Каким может быть наибольшее число сторон (невыпуклого) многоугольника, у которого ровно 8 внутренних углов больше 90º?
(А) 11
(Б) 16
(В) 20
(Г) 27
(Д) 30
Задача 29.
Рассматриваются квадратичные функции $y(x) = ax^2 + bx + c$ $(a ≠ 0)$, для которых $y(1) = 1$, $y(3) = −1$. Какое из утверждений неверно?
(А) если $c<1$, то $a<0$
(Б) если $a<0$, то $c<1$
(В) если $\displaystyle – \frac{b}{2a}<1$, то $a<0$
(Г) если $a<0$, то $\displaystyle – \frac{b}{2a}≤3$
(Д) если $c>2$, то $a>0$
Задача 30.
Окружность радиуса 1 катится без скольжения по окружности радиуса 2 с внутренней стороны. На меньшей окружности отмечена точка Р, которая в начальном положении совпадает с центром большей окружности. Какова траектория точки Р?
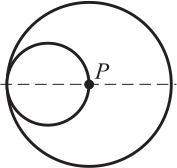
(А) 
(Б) 
(В) 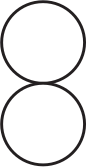
(Г) 
(Д) 

