Задача 1.
Какое наименьшее количество букв нужно вычеркнуть из фразы ВИВАТ КЕНГУРУ, чтобы оставшиеся буквы были различны и шли слева направо в алфавитном порядке?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 2.
Сколько получится слагаемых, если 210 записать как сумму двоек?
(А) 10
(Б) 32
(В) 512
(Г) 1024
(Д) 2048
Задача 3.
Джон думает, что если треугольник равнобедренный, то он остроугольный. Какой из следующих треугольников показывает, что Джон не прав?
(А)
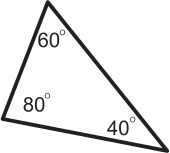
(Б)
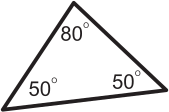
(В)
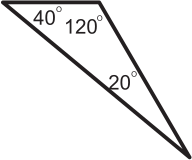
(Г)
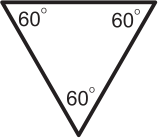
(Д)
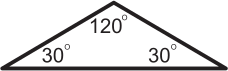
Задача 4.
Выражение $\sqrt{\sqrt{\sqrt{x}}}$ равно
(А) $\sqrt[8]{x}$
(Б) $\sqrt[6]{x}$
(В) $\sqrt[3]{x}$
(Г) $\sqrt[3]{x^2}$
(Д) $\sqrt{x^3}$
Задача 5.
Каково отношение закрашенной площади к белой?

(А) 2
(Б) 8/5
(В) 5/3
(Г) 3/2
(Д) 4/3
Задача 6.
Если разделить 40% от 2 на 2% от 40, то получится
(А) 20% от 1/20
(Б) 1% от 1
(В) 20% от 20
(Г) 1% от 100
(Д) 1% от 10
Задача 7.
Встречая Новый Год, Вася надел футболку с надписью  на груди и встал на руки (вверх ногами) перед зеркалом. Что увидел в зеркале его друг Коля, который стоял (на ногах) рядом с Васей?
на груди и встал на руки (вверх ногами) перед зеркалом. Что увидел в зеркале его друг Коля, который стоял (на ногах) рядом с Васей?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 8.
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники называются
(А) пропорциональными
(Б) похожими
(В) аналогичными
(Г) родственными
(Д) подобными
Задача 9.
Некоторые из нарисованных фигурок симметричны друг другу относительно одной из четырёх выделенных прямых. Сколько таких пар фигурок?
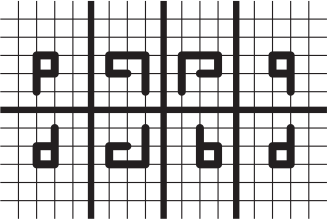
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 10.
Выражение aa ⋅ bb ⋅ cc ⋅ ab ⋅ bc ⋅ ca ⋅ ac ⋅ ba ⋅ cb равно
(А) (a + b + c)abc
(Б) (abc)abc
(В) (a + b + c)a+b+c
(Г) (abc)a+b+c
(Д) (abc)3a+3b+3c
Задача 11.
Какое из следующих чисел нельзя представить в виде произведения трёх чисел, одно из которых простое, а два других — составные?
(А) 25
(Б) 2 ⋅ 3 ⋅ 4 ⋅ 5
(В) 2 ⋅ 32 ⋅ 5
(Г) 6 ⋅ 12
(Д) 1000
Задача 12.
Прямоугольник ABCD пересекает окружность в точках E, F, G, H. Если АЕ = 4 см, EF = 5 см и DH = 3 см, то длина HG равна
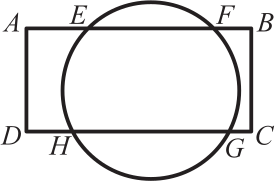
(А) 6 см
(Б) 7 см
(В) 20/3 см
(Г) 8 см
(Д) 9 см
Задача 13.
Сколько пар действительных чисел (a, b) таковы, что a + b = ab = $\displaystyle \frac{a}{b}$ ?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 14.
Коля шифрует числа: вместо каждой цифры он пишет сумму цифр её квадрата. Например, вместо 7 он пишет 13, так как 72 = 49 и 4 + 9 = 13, а вместо 2 пишет 4. Сколько чисел после шифровки могут превратиться в число 7910?
(А) 4
(Б) 6
(В) 8
(Г) 12
(Д) 16
Задача 15.
Два грузовика ехали по асфальтированной дороге со скоростью 80 км/ч, сохраняя дистанцию 24 м. Свернув на проселочную дорогу, каждый из них резко снизил скорость, и дистанция между ними стала равной 15 м. С какой скоростью поехали грузовики по проселочной дороге?
(А) 70 км/ч
(Б) 65 км/ч
(В) 60 км/ч
(Г) 55 км/ч
(Д) 50 км/ч
Задача 16.
Правильный треугольник разделён двумя прямыми на ромб площади 18, правильный треугольник площади 1 и две равные трапеции. Какова площадь каждой трапеции?
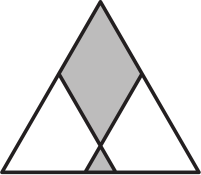
(А) 10
(Б) 12,5
(В) 15
(Г) 16
(Д) 18
Задача 17.
Если −2 ≤ x ≤ 5, −3 ≤ y ≤ 7, 4 ≤ z ≤ 8 и w = xy − z, то наименьшее возможное значение w равно
(А) −43
(Б) −23
(В) −22
(Г) −2
(Д) 2
Задача 18.
Произведение катетов прямоугольного треугольника с острым углом 15° равно
(А) трети квадрата гипотенузы
(Б) половине квадрата гипотенузы
(В) квадрату гипотенузы
(Г) квадрату четверти гипотенузы
(Д) квадрату половины гипотенузы
Задача 19.
Какое наибольшее число рёбер шестиугольной призмы может пересечь плоскость, не проходящая через вершины призмы?
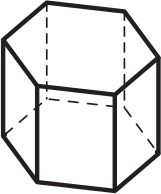
(А) 6
(Б) 7
(В) 8
(Г) 10
(Д) 12
Задача 20.
У флориста (составителя букетов) имеются розы: 84 красные, 24 белые и 36 жёлтых. Какое наибольшее количество одинаковых букетов он может составить, если хочет использовать все имеющиеся розы?
(А) 4
(Б) 6
(В) 8
(Г) 12
(Д) 18
Задача 21.
В числовом ребусе KAN − GAR = OO разным буквам соответствуют разные цифры, одинаковым — одинаковые. Найдите цифру N, если известно, что число KAN — самое большое из возможных.
(А) 8
(Б) 7
(В) 6
(Г) 5
(Д) 4
Задача 22.
На чертеже изображены графики двух линейных функций f и g. Пусть h(x) = f(x) ⋅ g(x). Какое из утверждений ложно?
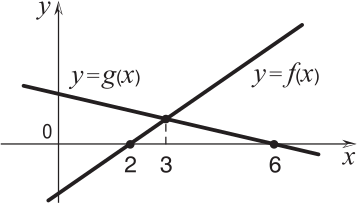
(А) h(x) < 0 при x < 2
(Б) На отрезке [5; 6] функция h убывает
(В) Функция h принимает наибольшее значение в точке х = 3
(Г) График y = h(x) имеет ось симметрии
(Д) Уравнение h(x) = −100 имеет два корня
Задача 23.
4 одинаковых кубика сложены так, как показано на рисунке. У кубика нет двух граней с одинаковым числом точек. Сколько точек на левой грани самого левого кубика?
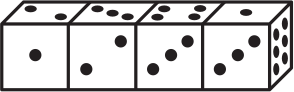
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) невозможно определить
Задача 24.
Через точку на плоскости провели n прямых. Среди углов между этими прямыми встречаются углы 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°. Каково наименьшее из возможных значений n?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 25.
Окружности радиусов 1, 2 и 3 попарно касаются друг друга. Какова длина выделенной дуги?
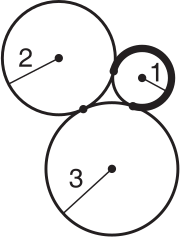
(А) 3π/2
(Б) 5π/2
(В) π/2
(Г) 5π/4
(Д) 2π/3
Задача 26.
Пусть М — произведение периметра треугольника на сумму длин трёх его высот. Площадь треугольника равна 1. Какое из утверждений неверно?
(А) М может быть больше 1000
(Б) всегда М > 6
(В) М может быть меньше 12
(Г) М может быть равно 18
(Д) если треугольник прямоугольный, то M > 16
Задача 27.
Робот выполняет одну операцию: натуральное число n он заменяет на сумму n + k, где k — наибольший делитель числа n, отличный от n. Робот начинает с чётного числа n, не кратного 4. Какое число получится после 10 шагов?
(А) 10n
(Б) 5n
(В) 3n
(Г) $\displaystyle \frac{41}{2}$n
(Д) $\displaystyle \frac{81}{2}$n
Задача 28.
Найдите α.
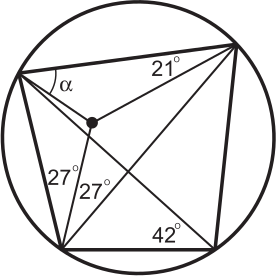
(А) 21°
(Б) 30°
(В) 36°
(Г) 42°
(Д) невозможно определить
Задача 29.
В клетки квадрата 3 × 3 требуется вписать девять различных натуральных чисел так, чтобы все они не превосходили n, и чтобы произведения чисел в каждой строке и каждом столбце были равны. При каком наименьшем n это возможно?
(А) 16
(Б) 15
(В) 14
(Г) 12
(Д) 9
Задача 30.
$\displaystyle \left(x^2 − x + \frac{5}{4}\right)⋅\left(y^2 + 3y + 3\right) = \frac{3}{4}$. Чему равно $x + y$ ?
(А) −1
(Б) 0
(В) 1
(Г) 2
(Д) невозможно определить

