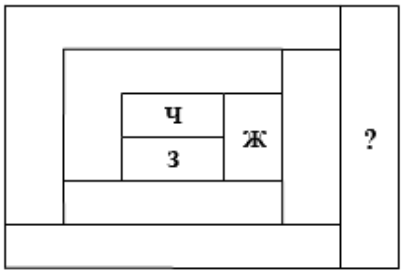
Каждую область на схеме ниже красят одним из четырёх цветов: чёрным (Ч), зелёным (З), жёлтым (Ж) или синим (С). При этом две области, имеющие общий отрезок границы, нельзя красить в один и тот же цвет. При условии, что центральные области окрашены так, как это показано на рисунке, в какой цвет может быть окрашена крайняя правая область?

«Динамо» сыграло 6 матчей: 1 матч команда выиграла, 2 свела вничью и 3 проиграла. Всего во всех играх динамовцы забили 5 голов и пропустили 3 мяча. С каким счётом мог завершиться матч, в котором «Динамо» победило?

Света и Алёна играли на конфетки. Сначала Алёна проиграла половину своих конфеток Свете, потом Света проиграла 4 конфеты, потом снова Алёна проиграла треть своих Свете. В итоге у Алёны оказалось 34 конфетки, а всего у девочек в самом начале было 100 конфеток. Сколько конфет было у каждой девочки до начала игры?

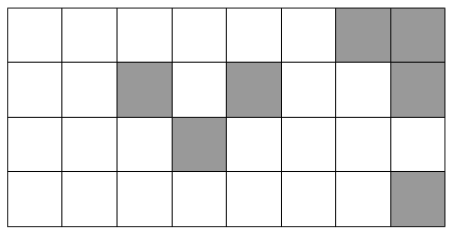
Можно ли разрезать фигуру на рисунке на различные фигурки из пяти клеток? (Серые клетки вырезаны.)

В вазе лежат конфеты. Один школьник может съесть не более семи конфет. Чтобы съесть все конфеты из вазы необходимо четыре школьника. Когда в вазу положили ещё 11 конфет, пришлось звать на помощь ещё двух школьников. Какое наименьшее количество конфет могло быть в вазе первоначально?

Лука, Ярослав и Егор решали задачи. Лука решил в 2 раза больше, чем Егор, но в одной задаче ошибся, а Ярослав решил в 3 раза больше, чем Егор, но ошибся в пяти задачах. Оказалось, что у Ярослава и Луки поровну правильно решённых задач. Сколько задач решил Егор, если он решил все задачи верно?