Задача 1.
Можно ли на прямой отметить точки 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 так, чтобы расстояния между ними были равными: 𝐴𝐵 = 6, 𝐵𝐶 = 7, 𝐶𝐷 = 1, 𝐷𝐸 = 9, 𝐴𝐸 = 12?
Задача 2.
У продавца есть чашечные весы. Помогите продавцу придумать набор из 4 гирь, с помощью которых он сможет взвешивать на этих весах любое целое число килограммов от 1 до 12. (При каждом взвешивании можно использовать не более двух гирь; гири можно ставить на разные чашки весов.)
Задача 3.
Разрежьте фигуру на 5 четырёхклеточных фигурок различной формы таким образом, чтобы в каждой из пяти фигур присутствовала ровно одна красная клетка.
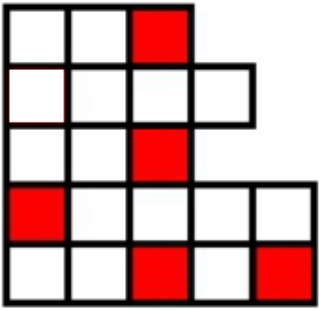
Задача 4.
Можно ли покрасить 33 клетки доски 7×7, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна соседствовать ни с одной другой ранее закрашенной клеткой?
Задача 5.
У числа 2018 нашли сумму цифр — 11. Потом нашли произведение цифр получившегося числа — получили 1. Сколько ещё таких лет в 21 веке, обладающих таким же свойством?
Задача 6.
Можно ли на каждое поле шахматной доски поставить белого или чёрного короля так, чтобы каждый король бил больше королей чужого цвета, чем своего, а общее количество белых и чёрных королей была разной?

