Задача 1.
Можно ли отметить на плоскости по 5 оранжевых, 5 фиолетовых и 5 салатовых точек, все расстояния между которыми различны, так, чтобы для каждой оранжевой точки ближайшая к ней цветная была фиолетового цвета, для каждой фиолетовой точки — ближайшая салатового цвета, а для каждой салатовой точки — ближайшая оранжевого цвета?
Задача 2.
Разрежьте фигуру на 5 четырёхклеточных фигурок различной формы таким образом, чтобы в каждой из пяти фигур присутствовала ровно одна красная клетка.
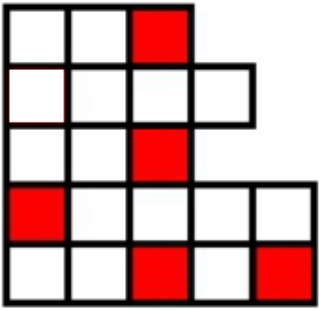
Задача 3.
На школьной дискотеке Василий, Николай, Владимир и Алексей, все из разных классов, танцевали с девочками, но каждый танцевал не со своей одноклассницей. Лена танцевала c Василием, Аня — с одноклассником Наташи, Николай — с одноклассницей Владимира, а Владимир — с Олей. Кто с кем учится в одном классе?
Задача 4.
Среди поваров несколько лентяев, а остальные — трудолюбивые люди. Лентяи никогда не говорят правду и всегда отвечают либо «суббота», либо «воскресенье». Трудолюбивые повара говорят только правду, когда здоровы, и ведут себя как лентяи, когда болеют. Каждый день в течение недели, с понедельника по воскресенье, каждому повару задавали вопрос: «Какой сегодня день недели?» В результате 25 раз прозвучали слова «суббота» или «воскресенье», и 31 раз другие дни. Какое максимальное число лентяев может быть среди поваров?
Задача 5.
За круглым столом сидят 2018 человек. Каждый из них – рыцарь, который всегда говорит правду, или лжец, который всегда лжёт. Оказалось, что рядом с каждым лжецом сидит ровно один лжец. Каждого из сидящих за столом спросили, сколько лжецов сидит рядом с ним. Получили только ответы «один» и «два». Какое наименьшее количество лжецов может сидеть за столом?
Задача 6.
В турнире участвовало 10 ребят. Каждый день из ребят составлялось 5 пар и ребята из каждой пары играли друг с другом одну партию. Всего каждый из ребят поиграл с каждым только раз, при этом не меньше чем в половине всех партий игроки были односельчанами (из одного села). Докажите, что в каждом туре хотя бы одна партия была между односельчанами.

