Задача 1.
Сколькими различными способами из шестиклеточной фигуры «лесенка» можно вырезать 2 клетки так, чтобы фигура осталась связной?
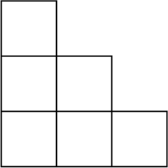
Задача 2.
Разрежьте квадрат 6×6 клеток на две части так, чтобы у первой части площадь была на 2 клетки больше, чем у второй, а у второй части периметр был на 2 больше, чем у первой. (Резать можно только по сторонам клеток. Длина стороны клетки равна 1.)
Задача 3.
Найдите наименьшее десятизначное число, состоящее из попарно различных цифр, у которого сумма первых двух цифр равна сумме последних трёх цифр.
Задача 4.
Найдите последнюю цифру значения выражения 12 + 22 + 32 + . . . + 20192.
Задача 5.
В комнате находится 10 человек, некоторые из них всегда говорят правду, а остальные всегда лгут. На каждого из них надета чёрная или белая шапка. Каждый из них сказал: «Среди остальных 9 человек (всех, кроме меня) ровно трое носят чёрные шапки.» Сколько из них может быть лжецами?
Задача 6.
Разрежьте фигуру, изображённую на рисунке, на 4 одинаковые по форме и площади части. Резать можно только по сторонам клеточек. Части можно поворачивать и переворачивать.
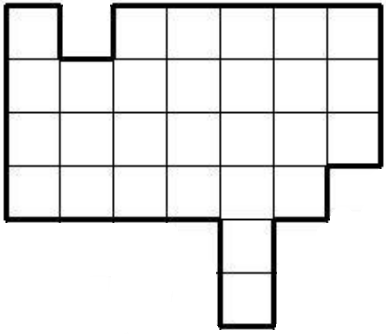
Задача 7.
У Антона есть две цистерны объёмом 1001 литров и 26 литров. Он может набирать воду из реки и переливать воду из цистерны в цистерну. Сколько различных ненулевых объемов воды он может отмерить в цистерне с объёмом 1001 л?
Задача 8.
В мешке лежат белые, синие, красные шарики (как патриотично!), если вытащить любые 10 шариков из мешка, среди них точно найдётся белый шарик. Перечислите все возможные варианты количества красных шариков в мешке.

