Задача 1.
Василиса Прекрасная раскладывала гребни по шкатулкам. Попыталась разложить поровну по двум шкатулкам — один лишний гребень остался. Попробовала то же с трёмя шкатулками — опять один лишний. Достала четвёртую шкатулку — не получается поровну разложить, снова один гребень лишний. Попыталась разложить гребни по пяти шкатулкам — в этот раз осталось два лишних. Василиса всплеснула руками и отказалась от своей затеи.
Какое наименьшее число гребней могло быть у Василисы?
Задача 2.
Путь из деревни А в деревню Б проходит через холм, на вершине которого стоит деревня М. При подъёме на холм почтовая карета едет со скоростью 10 км/ч, при спуске — 20 км/ч. Из А в Б карета едет 2 часа, из Б в А — 2,5 часа.
Отметьте все верные утверждения:
- средняя скорость движения от Б до А равна 15 км/час
- дорога от А до М короче, чем от Б до М
- время движения от А до М в 2 раза меньше времени движения от М до Б
- время движения от Б до М в 4 раза больше, чем от М до А
- расстояние от А до Б больше, чем 32 км
- расстояние от А до М в 2 раза меньше расстояния от М до Б
- вся дорога составляет 30 км
Задача 3.
В уезде живут только купцы и разбойники. Разбойники врут только если у них есть деньги, а купцы врут только если у них нет денег. Между четырьмя жителями уезда состоялся такой разговор:
- Первый: «У меня есть деньги!»
- Второй: «Ты врёшь!»
- Третий: «Вы оба врёте!»
- Четвёртый: «Третий, ты врёшь! Деньги есть только у меня и тебя».
Отметьте все верные утверждения:
- первый может быть купцом
- первый может быть только разбойником
- среди четверых жителей есть хотя бы один купец
- среди четверых жителей только два разбойника
- среди четверых жителей есть три купца
- среди четверых жителей только у одного есть деньги
- четвёртый может быть только купцом
- третий может быть и купцом, и разбойником
- второй не мог сказать правду
- у четвёртого не могло быть денег
Задача 4.
Впишите во все клетки квадрата, кроме центральной, все целые числа от 1 до 8 так, чтобы сумма чисел в любых пяти клетках, образующих угол квадрата, была равна 22. Например, клетки с номерами 1, 2, 3, 7, 8 образуют левый верхний угол.
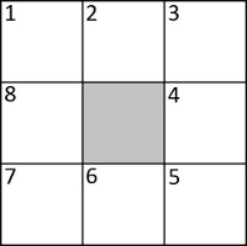
Задача 5.
Несколько древних русских богатырей (в том числе и Добрыня Никитич) устроили турнир по армрестлингу. Никакие два богатыря, сразившись друг с другом, повторно между собой не сражаются. Известно, что каждый богатырь сразился хотя бы с одним богатырём. Всего было проведено семь матчей. Богатырь соревновался с Добрыней Никитичем тогда и только тогда, когда соревновался с чётным числом соперников.
Сколько богатырей могло принять участие в турнире?

