Задача 1.
ответНапишите вместо семи звёздочек семь различных цифр так, чтобы получилось верное равенство:
∗∗∗∗ + ∗∗ + ∗ = 2015
Задача 2.
ответТребуется разрезать фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. При этом должно получиться ровно два трёхклеточных уголка, а остальные — четырёхклеточные. Покажите, как это сделать.
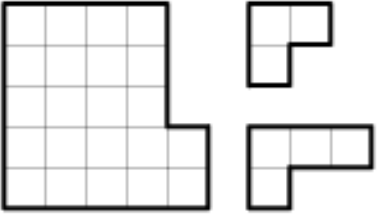
Задача 3.
ответНа столе лежат конфеты трёх видов: ириски, карамельки и леденцы. Известно, что ирисок на 8 меньше, чем всех остальных конфет, а карамелек — на 14 меньше, чем всех остальных конфет. Сколько леденцов лежит на столе? Обязательно объясните свой ответ.
Задача 4.
ответ- Разбейте натуральные числа от 1 до 10 на пары так, чтобы разность чисел в каждой паре была равна 2 или 3.
- Можно ли натуральные числа от 1 до 2014 разбить на пары так, чтобы разность чисел в каждой паре была 2 или 3?
Задача 5.
ответВ волшебной кофейне встретились 55 существ: эльфов и гномов. Каждый заказал себе либо чашку чая, либо чашку кофе. Все эльфы говорят правду, когда пьют чай, и обманывают, когда пьют кофе, а все гномы — наоборот. На вопрос «Вы пьёте чай?» ответили «да» 44 присутствующих, на вопрос «Вы гном?» — 33. А на самом деле — сколько из собравшихся пили чай и сколько среди собравшихся было гномов? Обязательно объясните свой ответ.
