Задача 1.
Сравните числа: 20162016 ⋅ 201720172017 и 20172017 ⋅ 201620162016.
Задача 2.
За одну операцию от многоугольника отрезают по прямой равнобедренный треугольник и выкидывают. Нарисуйте на клетчатой бумаге квадрат (удобного вам размера) и за несколько таких операций получите из него кусок в виде прямоугольника, одна из сторон которого в 7 раз больше другой.
Задача 3.
Стоит шеренга из 10 эльфов, а перед ней — шеренга из 10 гномов. Перед каждым эльфом стоит гном ростом ниже. Докажите, что если шеренгу эльфов построить по росту (слева направо), и шеренгу гномов построить по росту (слева направо), то снова перед каждым эльфом будет гном ростом ниже.
Задача 4.
В некоторые клетки доски 10 × 10 поставили по фишке так, что на каждой вертикали и на каждой горизонтали стоит ровно одна фишка. Затем доску разделили на четыре квадрата 5 × 5. Докажите, что в левом верхнем квадрате стоит столько же фишек, сколько в правом нижнем квадрате.
Задача 5.
Петя и Вася играют. На столе лежат две кучки камней — в одной 100 штук, а в другой — 79. Ходят по очереди, начинает Петя. За ход игрок одну из куч убирает со стола целиком, а оставшуюся кучу делит на столе на две кучи произвольным образом. Проигрывает тот, у кого нет хода (остались две кучи по 1 камню). Кто может обеспечить себе победу и как ему играть?
Задача 6.
Все фантики Кати лежат в трёх коробках (пустых коробок нет). Две десятых её фантиков лежат в первой коробке, несколько седьмых — во второй, и ещё 33 фантика — в третьей. Сколько всего фантиков у Кати?
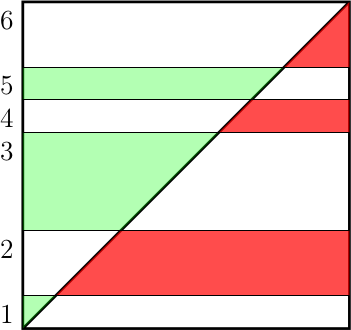
Задача 7.
Сторона квадрата разбита на 6 отрезков. Сумма длин 1-го, 3-го и 5-го отрезков равна сумме длин 2-го, 4-го и 6-го отрезков. Через концы отрезков провели прямые, параллельные другой стороне квадрата, а также провели диагональ (см. рисунок). Докажите, что сумма площадей светло-серых «полосок» равна сумме площадей тёмно-серых «полосок».