Задача 1.
На столе лежали три стопки одинаковых монет из 19 монет, 23 монет и 29 монет. В одной из них одну монет заменили монетой другого веса, внешне не отличающейся от остальных. Есть чашечные весы без гирь. На чаши можно класть кучки монеты и сравнивать вес этих кучек. Как за одно взвешивание найти стопку, в которой все монеты одинаковые?
Задача 2.
Мотоциклист и велосипедист выехали одновременно из А в В. Проехав треть пути, велосипедист остановился. Когда велосипедист продолжил движение, мотоциклисту оставалось проехать треть пути до В. Мотоциклист, доехав до В, без остановки поехал обратно в А. Кто приедет раньше: мотоциклист в А или велосипедист в В?
Задача 3.
В детском саду дети, построенные парами, возвращаются с вечернего чая с пряниками в карманах. В каждой паре идут мальчик и девочка, причём у мальчика пряников либо вдвое больше, либо вдвое меньше, чем у девочки. Могут ли они все вместе иметь ровно 2006 пряников?
Задача 4.
В отрывном календаре оторвали листок и положили на следующий так, как показано на рисунке. Какая часть нижнего листка больше: закрытая или незакрытая?
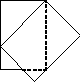
Задача 5.
На чудесной сосне растут 8 бананов и 7 апельсинов. Если сорвать два одинаковых фрукта, на сосне тут же вырастает ещё один банан, а если сорвать два разных, то вырастает один апельсин. Срывать фрукты по одному нельзя. Можно ли так срывать фрукты с сосны, чтобы последний фрукт на ней был бананом?

