На доске написано число 2012. За один ход можно увеличить или уменьшить число на доске на произведение любых двух его цифр. Можно ли такими операциями получить из числа 2012 число 2011?

На острове рыцарей и лжецов по маршруту из трёх остановок ходит автобус. Три местных жителя – пассажиры автобуса – заспорили, какая сейчас остановка.

• Первый: «Сейчас А. Следующая Б».
• Второй: «Нет, Б уже была. Сейчас С».
• Третий. «Да сейчас С. Но Б только ещё будет».

Какая сейчас остановка?

Два прямоугольных листа бумаги совместили, как показано на рисунке.

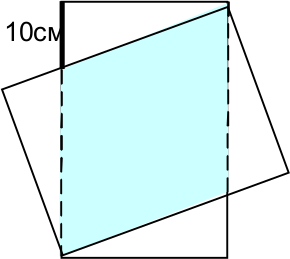
Оказалось, что длина выделенного жирным отрезка равна 10 см. Сравните что больше – площадь «двойной» части (закрашенной на рисунке) или «одинарной» (из четырёх кусочков), если длина листа бумаги 30 см.

Дети встали в круг. Оказалось, что у пятерых оба соседа – мальчики, ещё у двоих соседи разного пола, у остальных же оба соседа – девочки. Сколько было мальчиков среди детей?

Принцесса вошла в замок через главные ворота, а вышла через одни из шести запасных (они отмечены на плане буквами А, В, С, D, E, F, G).

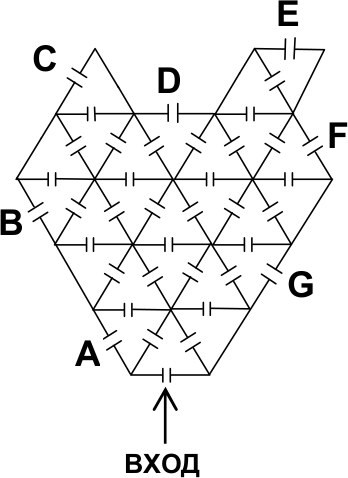
Принцесса прогулялась по 15 комнатам, не побывав ни в одной дважды. Через какие ворота могла выйти принцесса? Укажите все варианты.