Можно ли, используя числа 2, 3, 4, 5, 6, 7, 8, 9, 10, составить три несократимые дроби $\displaystyle \frac{a}{b}$, $\displaystyle \frac{c}{d}$ и $\displaystyle \frac{e}{f}$ такие, что $\displaystyle \frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f} = 1$. Каждое число можно использовать один раз или не использовать вовсе.

Сложите из семи прямоугольников размерами 1 × 1, 1 × 2, 1 × 3, 1 × 4, 1 × 5, 1 × 6, 1 × 7 клеток два прямоугольника одинаковой площади, но разного периметра.

У шестиклассниц Светы и Юли одинаковое количество тетрадей. Они купили одинаковые наборы наклеек. Света наклеила на 5 тетрадей по одной наклейке, а на оставшиеся тетради – по 5 наклеек. Юля наклеила на 17 тетрадей по одной наклейке, а на оставшиеся тетради – по 17 наклеек. Сколько наклеек было в наборе, если Света и Юля использовали свои наборы наклеек полностью?

Бельчонок, зайчонок и лисёнок играют в игру.

• Лисёнок сказал: «Зайчонок глупее бельчонка».
• Зайчонок сказал: «Бельчонок выиграл».
• Бельчонок сказал: «Зайчонок не выиграл».

Оказалось, что солгал ровно один из трёх зверей – самый глупый. Самый умный зверь выиграл игру. Кто он?

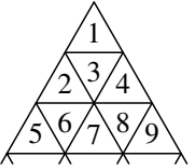
Каждая сторона равностороннего треугольника разбита на несколько равных частей по 1 см. Через точки деления проведены прямые, параллельные сторонам. Вася расставляет по строкам слева направо натуральные числа, начиная с 1 (см. рисунок). Его друг Петя выбрал горизонтальный отрезок, являющийся общей стороной двух маленьких треугольников. В одном из этих треугольников оказалось число 430. Какое число стоит в другом?