Задача 1.
Круглые сутки Кенгуру смотрит на свои новые электронные часы, которые показывают часы и минуты (от 00:00 до 23:59). Сколько раз за сутки он увидит на табло четыре цифры 2, 0, 0, 6 (в каком-нибудь порядке)?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 2.
Сколько из чисел $\sqrt{(−7)^2}$, $(−\sqrt{7})^2$, $−(\sqrt{7})^2$, $(−\sqrt{7})^{−2}$, $\left(7^{−2}\right)^2$ равны 7 ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 3.
Каких чисел не бывает?
(А) простых
(Б) натуральных
(В) рациональных
(Г) естественных
(Д) действительных
Задача 4.
Окружность разделена на 4 дуги, длины которых равны 2, 5, 6 и х. Дуга длины 2 соответствует центральному углу в 30º. Найдите величину х.
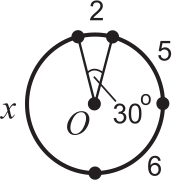
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 5.
Скучая на уроке, отличник Петя заметил, что муха ползёт по столу со скоростью 10000 миллиаршин в килосекунду. Один аршин равен 71 сантиметру. Определите скорость мухи в метрах в секунду.
(А) 7,1
(Б) 0,71
(В) 0,071
(Г) 0,0071
(Д) 0,00071
Задача 6.
Сколько нечётных среди чисел 1015 ⋅ 1510, 1515 + 1010, 1510 ⋅ 1515, 1510 + 1515 ?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 7.
Предположим, что фраза «Завтра будет лучше, чем вчера» верна каждый день. Какое из утверждений может тогда быть неверным?
(А) Послезавтра будет лучше, чем сегодня.
(Б) Сегодня будет лучше, чем позавчера.
(В) Послезавтра будет лучше, чем позавчера.
(Г) Завтра будет лучше, чем позавчера.
(Д) В 2006 году 1 апреля будет лучше, чем 16 марта.
Задача 8.
5% от 3% от числа 8 составляют 3% от 4% от числа:
(А) 5
(Б) 10
(В) 2,5
(Г) 8
(Д) другой ответ
Задача 9.
Какой может быть развёртка изображённого ниже кубика?
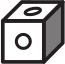
(А) 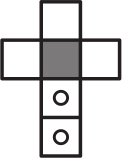
(Б) 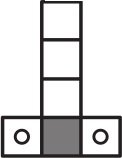
(В) 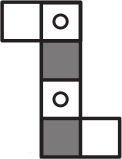
(Г) 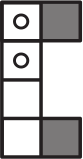
(Д) 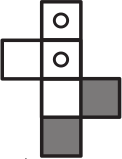
Задача 10.
Окружности радиусов 3 см и 5 см расположены так, что у них ровно три общие касательные. Тогда расстояние между центрами окружностей
(А) меньше 2 см
(Б) равно 2 см
(В) равно 4 см
(Г) равно 8 см
(Д) больше 8 см
Задача 11.
Решая одну из задач конкурса «Кенгуру», Коля обнаружил следующее: если ответ А верен, то и ответ В тоже верен; если ответ С неверен, то и ответ В неверен; если ответ В неверен, то оба ответа D и Е неверны. Как обычно, верен только один из ответов к задаче. Какой?
(А) А
(Б) В
(В) С
(Г) D
(Д) Е
Задача 12.
Прямые y = 2 x + 3 и y = kx − 3 пересекаются в первой четверти, причём ниже прямой y = 5. Тогда обязательно:
(А) k ≤ 0
(Б) 0 < k ≤ 2
(В) 2 < k ≤ 5
(Г) 5 < k ≤ 8
(Д) k > 8
Задача 13.
Если n – число рёбер некоторой призмы, то
(А) n обязательно чётно
(Б) n обязательно нечётно
(В) n обязательно делится на 3
(Г) n обязательно больше 10
(Д) n может равняться 2006
Задача 14.
Если а = $11^{(-12)^13}$, то
(А) а – большое положительное число
(Б) а близко к 1
(В) а положительно и близко к 0
(Г) а отрицательно и близко к 0
(Д) а – большое по модулю отрицательное число
Задача 15.
Пусть О — центр окружности, описанной около треугольника АВС. Найдите больший угол треугольника АВС, если АOВС — ромб.
(А) 90º
(Б) 100º
(В) 110º
(Г) 120º
(Д) 150º
Задача 16.
Какой из следующих фактов опровергает утверждение «Все простые числа, оканчивающиеся на 1, меньше 100»?
(А) 11 меньше 100
(Б) 13 – простое число
(В) 103 больше 100
(Г) 111 больше 100
(Д) 101 больше 100
Задача 17.
Семья Добсонов состоит из папы, мамы и нескольких детей. Средний возраст членов семьи – 18 лет. Без 38-летнего папы средний возраст – 14 лет. Сколько детей в этой семье?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 18.
Какое самое маленькое значение может принимать периметр неравнобедренного треугольника с целыми длинами сторон?
(А) 3
(Б) 4
(В) 6
(Г) 9
(Д) 10
Задача 19.
Квадрат PQRS со стороной 2 «катится» вдоль прямой l, пока точка P не вернётся на эту прямую. Каждый раз квадрат поворачивается вокруг правой нижней вершины. Какова длина пути, пройденного точкой P ?
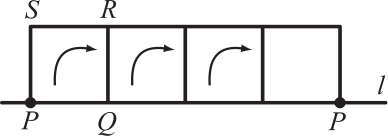
(А) 3π
(Б) π + π√2
(В) 2π + π√2
(Г) π + 2π√2
(Д) 2π + 2π√2
Задача 20.
Из четырёх спичек длины 1 сложили прямоугольный треугольник, разломав предварительно одну из спичек на две части. Чему может равняться площадь такого треугольника?
(А) 2/3
(Б) 1/2
(В) 3/4
(Г) 9/10 или 8/9
(Д) таких треугольников нет
Задача 21.
Пусть E(n) — сумма нечётных цифр числа n. Например, Е(82) = 0, Е(7) = 7, Е(3245) = 3 + 5 = 8. Найдите Е(1) + Е(2) + … + Е(100).
(А) 359
(Б) 400
(В) 500
(Г) 501
(Д) 721
Задача 22.
Если сумма четырёх положительных чисел равна 20, то произведение двух бóльших из этих чисел обязательно
(А) меньше 99
(Б) больше 0,001
(В) не равно 25
(Г) не равно 75
(Д) ни один из ответов А-Г не подходит
Задача 23.
Пусть α, β, γ — углы треугольника. Если sin2α + sin2β = sin2γ, то обязательно
(А) α = β = γ
(Б) α + β = γ
(В) α − β = γ
(Г) α2 + β2 = γ2
(Д) α + β = 2γ
Задача 24.
На заседании международного жюри конкурса «Кенгуру» за круглым столом сидят 12 человек. При этом на любых шести последовательных местах сидят представители не более, чем трёх разных стран. Представители какого наибольшего количества стран могут сидеть за столом?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 25.
Число $\sqrt{1 + 2005\sqrt{1 + 2004\sqrt{1 + 2003⋅2001}}}$ равно:
(А) 2002
(Б) 2003
(В) 2004
(Г) 2005
(Д) 2006
Задача 26.
Пусть g(x) — это функция, график которой изображён на рисунке. Каким может быть множество всех решений уравнения g(x) = f(x), если f(x) — некоторая нечётная функция?
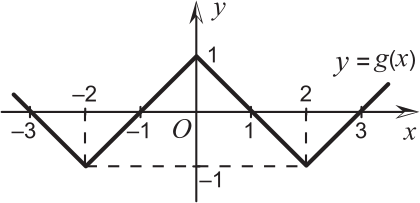
(А) x = 0, x = ±1
(Б) x = ±2
(В) х = 1, х = 2
(Г) x = ±1, x = 2
(Д) х = 0, х = 2
Задача 27.
Для скольких пар простых чисел (p, q) верно равенство pq + qp = 2q+1 + 1 ?
(А) 0
(Б) 1
(В) 2
(Г) 5
(Д) для бесконечно многих
Задача 28.
На какие фигуры нельзя разрезать правильный пятиугольник?
(А) на 5 треугольников
(Б) на 6 равнобедренных треугольников
(В) на трапеции
(Г) на шестиугольники
(Д) каждое из разрезаний А-Г возможно
Задача 29.
Какое из равенств может быть неверным, если $a^3 = a + 1$ ?
(А) $a^4 = a^2 + a$
(Б) $a^4 = a^3 + a^2 − 1$
(В) $a^4 = a^5 − 1$
(Г) $\displaystyle a^2 + a = \frac{1}{a − 1}$
(Д) $a^5 = a^4 − 1$
Задача 30.
На бумаге нарисованы два прямоугольных треугольника: синий и зелёный. Один из синих катетов вдвое длиннее одного из зелёных катетов, а зелёная гипотенуза в 3 раза длиннее синей. Что тогда невозможно?
(А) Другой зелёный катет в 4 раза длиннее другого синего катета.
(Б) Площадь зелёного треугольника в 10 раз больше площади синего.
(В) Площадь синего треугольника больше площади зелёного.
(Г) Один из углов зелёного треугольника равен 1º.
(Д) Один из углов синего треугольника больше 89º.

