Задача 1.
Сколько осей симметрии имеет рисунок?
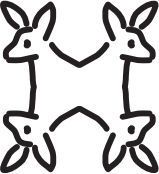
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) бесконечно много
Задача 2.
Числа a, b, c и d таковы, что a − 1 = b + 2 = c − 3 = d + 4. Какое из этих чисел наибольшее?
(А) a
(Б) b
(В) c
(Г) d
(Д) невозможно определить
Задача 3.
На клетчатом листочке отметили 6 точек (см. рисунок). Какой из следующих многоугольников не может иметь все вершины в отмеченных точках?

(А) квадрат
(Б) параллелограмм, не являющийся ромбом
(В) трапеция
(Г) тупоугольный треугольник
(Д) все многоугольники А-Г возможны
Задача 4.
На рисунке ∠AOD = 120°, ∠BOD = 3∠AOB и ∠AOC = 2∠COD. Чему равен ∠BOC ?
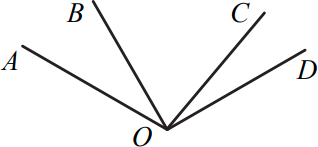
(А) 45°
(Б) 47°
(В) 50°
(Г) 57°
(Д) 60°
Задача 5.
Жан-Кристоф продолжает изучать русский язык. Он помнит, что, в отличие от неравенства 2009 ≤ 2010, неравенство 2009 < 2010 называется иначе. Как?
(А) твёрдым
(Б) сильным
(В) серьезным
(Г) точным
(Д) строгим
Задача 6.
Среди нескольких различных простых чисел ровно n% делятся на 3. Чему не может быть равно n ?
(А) 10
(Б) 20
(В) 25
(Г) 40
(Д) 50
Задача 7.
Если ac + ad + bc + bd = 68 и c + d = 4, то a + b + c + d равно
(А) 4
(Б) 17
(В) 21
(Г) 64
(Д) невозможно определить
Задача 8.
Какое из следующих чисел является наименьшим двузначным числом, не представимым в виде суммы трёх различных однозначных чисел?
(А) 10
(Б) 15
(В) 23
(Г) 25
(Д) 28
Задача 9.
Натуральные числа n и k > 1 таковы, что 22 ⋅ 44 ⋅ 55 = nk. Тогда
(А) k = 5
(Б) k = 4
(В) k = 3
(Г) k = 2
(Д) такое невозможно
Задача 10.
Известно, что все шесть цифр двух трёхзначных чисел p и q различны и p > q. Какое наименьшее значение может принимать разность p − q ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 11.
В четырёхугольнике ABCD стороны AD и BC равны, ∠DAC = 50°, ∠DCA = 65° и ∠ACB = 70°. Чему равен ∠ABC ?
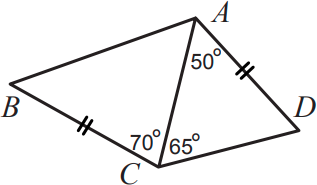
(А) 50°
(Б) 55°
(В) 60°
(Г) 65°
(Д) невозможно определить
Задача 12.
Андрей обмотал веревочкой плоскую пластинку, изображённую ниже. Как может выглядеть эта пластинка с противоположной стороны?
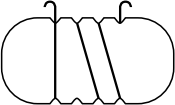
(А)
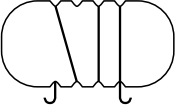
(Б)
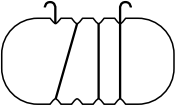
(В)
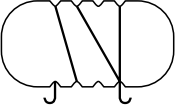
(Г)
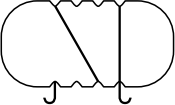
(Д)
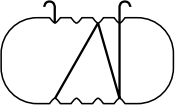
Задача 13.
В музыкальной школе количество участников конкурса «Кенгуру» составляет 5% от количества всех девочек и 20% от количества всех мальчиков. Сколько процентов учеников этой школы участвуют в конкурсе «Кенгуру»?
(А) 2%
(Б) 4%
(В) 5%
(Г) 8%
(Д) 12,5%
Задача 14.
Вася шифрует числа: вместо чётной цифры он рисует квадратик, а вместо нечётной — кружок. Если цифра делится на 3, то он закрашивает фигуру, а если не делится — оставляет фигурку незакрашенной. Так, число 56 превратится в картинку  . Сколько всего чисел превращается в эту же картинку?
. Сколько всего чисел превращается в эту же картинку?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 6
Задача 15.
Каким числом прямых можно разделить плоскость ровно на 5 областей?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) это невозможно
Задача 16.
Петя придумал две новые операции: $\displaystyle a\circ b = \frac{a^2 + b^2}{2}$ и $\displaystyle a\star b = \frac{a^2 − b^2}{2}$. Чему равно $(a\circ b)\star(ab)$ ?
(А) $\displaystyle \frac{\left(a^2 + b^2\right)^2}{8}$
(Б) $\displaystyle \frac{a^4 + b^4}{8}$
(В) $\displaystyle \frac{a^4 − b^4}{8}$
(Г) $\displaystyle \frac{\left(a^2 − b^2\right)^2}{8}$
(Д) 0
Задача 17.
На листе бумаги нарисована система координат. Вася согнул листок так, что точки с координатами (1; 5) и (7; 3) совпали. С какой точкой совпала точка (−1; −1) ?
(А) (4; 0)
(Б) (5; −3)
(В) (4; −3)
(Г) (5; −1)
(Д) (5; −2)
Задача 18.
Имеется семь последовательных натуральных чисел. Сумма первых трёх равна 33. Чему равна сумма последних трёх?
(А) 45
(Б) 42
(В) 39
(Г) 37
(Д) 36
Задача 19.
Дворник работает по вторникам, пятницам и нечётным числам. Какое наибольшее количество дней подряд он может работать?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 20.
Федя возвёл ненулевое число a в четвёртую степень, и оно увеличилось вдвое. Во сколько раз увеличится число a, если его возвести в десятую степень?
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 16
Задача 21.
На рисунке пять кругов пересекаются, образуя девять областей, в которые вписаны цифры от 1 до 9 (каждая цифра используется ровно 1 раз).
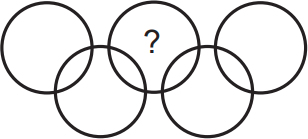
Оказалось, что сумма чисел, написанных в любом круге, равна 11. Какой может быть цифра, написанная в отмеченной области?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) так вписать цифры невозможно
Задача 22.
Бумажную полоску трижды сложили пополам, а потом разогнули. Что не могло получиться?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 23.
Из маленьких кубиков 1 × 1 × 1, каждый из которых целиком покрашен в один цвет, Кенгуру хочет сложить куб 3 × 3 × 3 так, чтобы любые два кубика, имеющие хотя бы одну общую вершину, были разных цветов. Какое наименьшее количество цветов потребуется для этого?
(А) 4
(Б) 6
(В) 8
(Г) 12
(Д) 27
Задача 24.
Равносторонний треугольник состоит из 36 маленьких равносторонних треугольников площади 1 (см. рисунок). Чему равна площадь треугольника ABC?
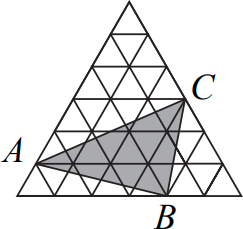
(А) 10
(Б) 11
(В) 12
(Г) 13
(Д) 14
Задача 25.
Прямые y = ax, y = bx и y = cx + d образуют треугольник, целиком лежащий в первой четверти. Что невозможно?
(А) c < 0 и d < 0
(Б) c > 0 и d < 0
(В) c < 0 и d > 0
(Г) c > 0 и d > 0
(Д) всё перечисленное возможно
Задача 26.
Про четырёхугольник ABCD известно, что ∠BAD = ∠CDA = 60°, ∠BDA = ∠CAB, AB = 2 и CD = 9 . Чему равно AD ?
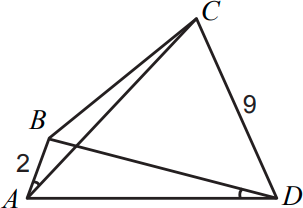
(А) 7
(Б) 10
(В) 11
(Г) 18
(Д) невозможно определить
Задача 27.
В Тридевятом царстве живут рыцари и лжецы. Каждая фраза рыцаря является истинной, а каждая фраза лжеца — ложной. Однажды несколько жителей царства сидели в комнате, и трое из них произнесли следующее.
- Первый: «В комнате не более 3 человек. Все они лжецы».
- Второй: «В комнате не более 4 человек. Не все из них лжецы».
- Третий: «В комнате ровно 5 человек.
Ровно трое из них — лжецы». Сколько в комнате лжецов?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) невозможно определить
Задача 28.
Два туриста вышли одновременно из села A в село B. Когда первый турист прошёл половину пути, второму осталось пройти 24 км, а когда второй прошёл половину пути, первому осталось пройти 15 км. Каково расстояние между A и B?
(А) 12 км
(Б) 36 км
(В) 40 км
(Г) 46 км
(Д) невозможно определить
Задача 29.
На рисунке α = 7°, а отрезки OA1, A1A2, A2A3, A3A4, … все равны между собой. Которая из точек Ak будет наиболее удалена от точки O ?
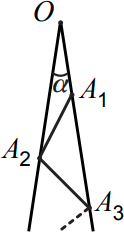
(А) A11
(Б) A12
(В) A13
(Г) A14
(Д) такой точки нет
Задача 30.
Наименьшее общее кратное чисел 24 и x меньше, чем наименьшее общее кратное чисел 24 и y. Чему не может быть равно отношение $\displaystyle \frac{y}{x}$ ?
(А) 7/8
(Б) 8/7
(В) 2/3
(Г) 7/6
(Д) 6/7

