Задача 1.
На рисунке показано, как слово КЕНГУРУ отражается в двух зеркалах. Что получится, если то же самое проделать с числом 2010?
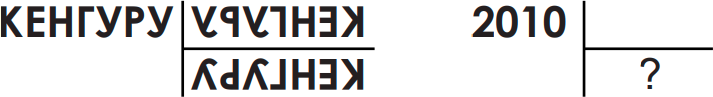
(А) 
(Б) 
(В) 
(Г) 
(Д) 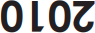
Задача 2.
В 2009 году мэром в Цветочном городе был Незнайка. В результате цены выросли на 10000%. Во сколько раз выросли цены?
(А) 10000
(Б) 1001
(В) 999
(Г) 101
(Д) 100
Задача 3.
На плоскости отметили 6 точек — вершины правильного шестиугольника. Какой из перечисленных многоугольников не может иметь все свои вершины в отмеченных точках?
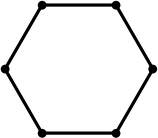
(А) правильный треугольник
(Б) прямоугольный треугольник
(В) прямоугольник
(Г) ромб
(Д) трапеция
Задача 4.
В отличие от неравенства 2010 < 2011, неравенство 2010 ≤ 2011 называется
(А) слабым
(Б) нестрогим
(В) неточным
(Г) мягким
(Д) несерьезным
Задача 5.
Найдите n, если 9n + 9n + 9n + 9n + 9n + 9n + 9n + 9n + 9n = 32010
(А) 502
(Б) 1004
(В) 1206
(Г) 1508
(Д) 2010
Задача 6.
Вася «шифрует» числа: вместо чётной цифры он рисует квадрат, вместо нечётной — круг. Если цифра делится на 3, он закрашивает соответствующую ей фигуру, а если не делится — оставляет белой. Так, число 23 превращается в картинку  . Сколько всего чисел превращаются в эту же картинку?
. Сколько всего чисел превращаются в эту же картинку?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 9
Задача 7.
Четырехугольник ABCE — квадрат, BCF и CDE — правильные треугольники, AB = 1. Найдите FD.
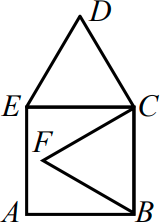
(А) $\sqrt{2}$
(Б) $\displaystyle \frac{\sqrt{3}}{2}$
(В) $\sqrt{3}$
(Г) $\sqrt{5} − 1$
(Д) $\sqrt{6} − 1$
Задача 8.
У Ивана много родственников. Отец отца сына Ивана — Василий, а отец отца Ивана — Николай. Как зовут отца сына отца Ивана?
(А) Василий Николаевич
(Б) Николай Васильевич
(В) Василий Иванович
(Г) Иван Васильевич
(Д) Иван Николаевич
Задача 9.
Среди нескольких различных простых чисел ровно n% делятся на 5. Чему не может равняться n ?
(А) 25
(Б) 20
(В) 15
(Г) 10
(Д) 5
Задача 10.
Придя в школу, каждый из пяти друзей отметил на координатной плоскости точку с такими координатами: время t, затраченное им на дорогу от дома до школы, и пройденное расстояние S. Кто из ребят шёл быстрее всех?
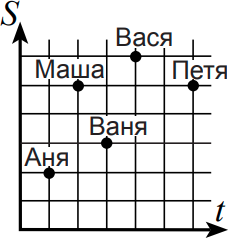
(А) Аня
(Б) Маша
(В) Ваня
(Г) Вася
(Д) Петя
Задача 11.
Если 2a − b = 505 и 3b − c = 333, то 4a + 7b − 3c равно
(А) 2009
(Б) 2010
(В) 999
(Г) 838
(Д) невозможно определить
Задача 12.
На сторонах АВ и АС треугольника АВС как на диаметрах построили окружности, которые пересекаются в точках А и Р. Тогда для треугольника ABC точка P обязательно является
(А) центром описанной окружности
(Б) центром вписанной окружности
(В) серединой ВС
(Г) основанием одной из высот
(Д) точкой пересечения медиан
Задача 13.
В кладовке имеются большие и маленькие коробки. В маленькую коробку помещается только один мяч, а в большую — два. 13 мячей можно разложить по коробкам так, чтобы осталось 9 пустых коробок. 10 мячей можно разложить по коробкам так, чтобы осталось 6 пустых коробок. Сколько коробок в кладовке?
(А) 6
(Б) 9
(В) 15
(Г) 16
(Д) 22
Задача 14.
На сколько частей делят координатную плоскость кривые $y = (x + 10)^2 − 20$ и $\displaystyle y = \frac{1}{x}$ ?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 15.
В музыкальной школе количество участников «Кенгуру» — это 6% от числа всех девочек и 30% от числа всех мальчиков. Сколько процентов учеников этой школы участвовали в конкурсе «Кенгуру»?
(А) 2%
(Б) 4%
(В) 5%
(Г) 7,5%
(Д) 10%
Задача 16.
Бумажную полоску трижды сложили пополам, а потом разогнули. Что не могло получиться?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 17.
Сколько натуральных чисел имеют сумму цифр 2010 и произведение цифр 2?
(А) 2010
(Б) 2009
(В) 2008
(Г) 1005
(Д) 1004
Задача 18.
Когда треугольник согнули по пунктирной линии, получилась фигура, изображённая справа. Площадь закрашенной области равна 1, а площадь исходного треугольника в 1,5 раза больше площади всей полученной фигуры. Найдите площадь исходного треугольника.
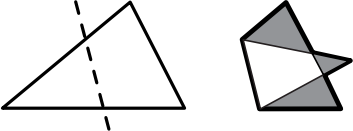
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) невозможно определить
Задача 19.
Дворник работает по вторникам, пятницам и нечётным числам. Какое наибольшее количество дней подряд он может работать?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 20.
На координатной плоскости отмечено 6 точек. Известно, что график функции f проходит через какие-то 4 из этих точек. Какой может быть функция f ?
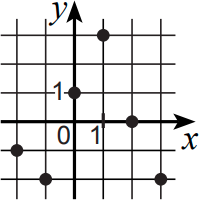
(А) чётной
(Б) нечётной
(В) возрастающей
(Г) убывающей
(Д) ни один из вариантов А-Г не подходит
Задача 21.
Для скольких чисел n из набора 1, 2, 3, …, 100 число nn является квадратом некоторого натурального числа?
(А) 5
(Б) 10
(В) 50
(Г) 54
(Д) 55
Задача 22.
Карлсон, Винни-Пух и Чебурашка съели торт. Они ели по очереди, и каждый из них ел столько времени, сколько понадобилось бы двум другим едокам, чтобы, «работая» вместе, съесть половину торта. Во сколько раз быстрее они съели бы торт, если бы ели все вместе, а не по очереди?
(А) 2
(Б) 2,5
(В) 3
(Г) 3,5
(Д) 4
Задача 23.
В равнобедренной трапеции ABCD точка Х — середина боковой стороны АВ, BX = 1, ∠CXD = 90°. Найдите периметр этой трапеции.
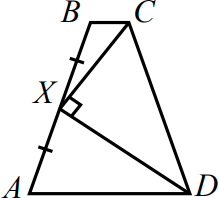
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) невозможно определить
Задача 24.
Про натуральное число m известно, что в десятичной записи числа m3 не менее 5 цифр, а в записи числа m8 не более 11 цифр. Сколько цифр в записи числа m24?
(А) 24
(Б) 29
(В) 32
(Г) 33
(Д) 34
Задача 25.
Штрих-код состоит из чередующихся чёрных и белых полос, причём первая и последняя полосы — чёрные. Ширина каждой полосы равна 1 или 2, а суммарная ширина штрих-кода должна равняться 12. Сколько существует различных штрих-кодов (читаемых слева направо) с такими свойствами?

(А) 12
(Б) 24
(В) 66
(Г) 108
(Д) 116
Задача 26.
Площадь выпуклого четырёхугольника равна 0,001 см2. Известно, что все его стороны и диагонали имеют длину не меньше 1 см, причём ровно k из них равны 1 см. Чему равно наибольшее возможное значение k ?
(А) 0
(Б) 3
(В) 4
(Г) 5
(Д) таких четырёхугольников не существует
Задача 27.
Число (2 + 3)⋅(22 + 32)⋅(24 + 34)⋅(28 + 38)⋅…⋅(22048 + 32048) + 24096 равно
(А) 62048
(Б) 24096 ⋅ 32048
(В) 34096
(Г) 36144
(Д) 34096 + 62048
Задача 28.
Ровно 1% солдат полка награждены медалями. Полк выстроили в форме прямоугольника. Оказалось, что награжденные солдаты встречаются ровно в 30% рядов и в 40% колонн. Какое наименьшее количество солдат может быть в этом полку?
(А) 100
(Б) 600
(В) 1000
(Г) 1200
(Д) 1500
Задача 29.
В четырёхугольнике ABCD известны некоторые углы между сторонами и диагоналями (см. рисунок). Найдите ∠ACD.
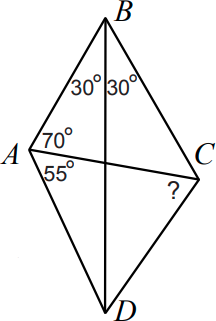
(А) 30°
(Б) 35°
(В) 45°
(Г) 65°
(Д) невозможно определить
Задача 30.
Сколькими способами произведение 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ 9 ⋅ 10 можно представить в виде суммы двух или более последовательных натуральных чисел?
(А) 29
(Б) 59
(В) 119
(Г) 239
(Д) другой ответ

