Задача 1.
Бабочку отразили зеркально относительно прямой b, а потом повернули на 90° против часовой стрелки вокруг кончика носа кенгуру (точки А). После этого бабочка оказалась у кенгуру:
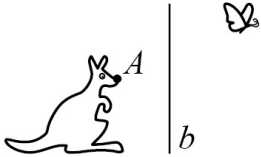
(А) на носу
(Б) на лапе
(В) на хвосте
(Г) на спине
(Д) в сумке
Задача 2.
Сумма цифр семизначного числа равна 6. Чему равно произведение цифр этого числа?
(А) 0
(Б) 5
(В) 6
(Г) 7
(Д) невозможно определить
Задача 3.
Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 40° и 70°?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 0
Задача 4.
Сколько копеек в децисантикилорубле?
(А) 0,1
(Б) 1
(В) 10
(Г) 100
(Д) 1000
Задача 5.
В Венеции каждый день происходит небольшое наводнение: вода поднимается, а потом отступает. На графике показано изменение уровня воды 6 мая 2011 года. Сколько часов в этот день уровень воды был выше 30 см?

(А) 5
(Б) 6
(В) 7
(Г) 9
(Д) 12
Задача 6.
Число, куб которого равен 201212, умножили на квадрат числа 201211. Что получилось?
(А) 201221
(Б) 201226
(В) 201231
(Г) 201258
(Д) 201288
Задача 7.
Жук Жак ползёт по координатной плоскости. Он стартует из точки (1; 1) и движется так, что произведение его координат не меняется. По какой линии ползёт жук?
(А) по прямой
(Б) по окружности
(В) по параболе
(Г) по гиперболе
(Д) по ломаной линии
Задача 8.
Часы лежат на столе циферблатом вверх. Минутная стрелка сейчас указывает на юго-восток. Через сколько минут она будет указывать на северо-восток?
(А) 15
(Б) 20
(В) 30
(Г) 40
(Д) 45
Задача 9.
Как гласит русская поговорка, ложка дёгтя портит бочку мёда. Сколько банок мёда удастся испортить десятью каплями дёгтя, если в бочке 40 банок, а в ложке 200 капель?
(А) 2
(Б) 4
(В) 5
(Г) 10
(Д) 20
Задача 10.
Про число x известно, что x3 < 64 < x2. Тогда
(А) 0 < x < 64
(Б) −8 < x < 4
(В) −4 < x < 8
(Г) x < −8
(Д) такого числа x не существует
Задача 11.
Фигура на рисунке образована двумя квадратами, треугольником, площадь которого равна 8 см2, и закрашенным параллелограммом. Чему равна площадь этого параллелограмма?
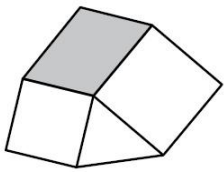
(А) 15 см2
(Б) 16 см2
(В) 18 см2
(Г) 20 см2
(Д) 21 см2
Задача 12.
Маша изучает натуральные числа, которые делятся на 72 и имеют в своей десятичной записи только нули и единицы. Сколько цифр в самом маленьком из таких чисел?
(А) 9
(Б) 11
(В) 12
(Г) 13
(Д) 14
Задача 13.
В семье пятеро мужчин: Иван Сидорович, Сидор Иванович, Сидор Петрович, Пётр Сидорович и Пётр Петрович. Один из них сейчас смотрит в окно, его отец спит, брат читает книгу, а сыновья ушли гулять. Как зовут того, кто смотрит в окно?
(А) Иван Сидорович
(Б) Сидор Иванович
(В) Сидор Петрович
(Г) Пётр Сидорович
(Д) Пётр Петрович
Задача 14.
Две стороны четырёхугольника равны 1 и 7. Одна из диагоналей, длина которой равна 3, делит его на два равнобедренных треугольника. Чему равен периметр этого четырёхугольника?
(А) 12
(Б) 14
(В) 16
(Г) 18
(Д) 20
Задача 15.
Натуральные числа a и b таковы, что a + b = 2012. Какое из следующих равенств возможно при некотором натуральном k?
(А) 2a ⋅ 3b = 12k
(Б) 2a ⋅ 3b = 18k
(В) 2a ⋅ 3b = 36k
(Г) 2a ⋅ 3b = 72k
(Д) 2a ⋅ 3b = 48k
Задача 16.
Число x отрицательно, а число y положительно. Что не может произойти, если x увеличить, а y — уменьшить?
(А) x + y увеличится
(Б) x/y уменьшится
(В) y/x уменьшится
(Г) y − x уменьшится
(Д) x − y уменьшится
Задача 17.
На какое наименьшее число тупоугольных треугольников можно разрезать квадрат?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) это невозможно сделать
Задача 18.
Какое из утверждений А-Г неверно?
(А) произведение любых двух нечётных чисел — нечётное число
(Б) произведение любых двух нечётных функций — нечётная функция
(В) произведение любых двух чётных чисел — чётное число
(Г) произведение любых двух чётных функций — чётная функция
(Д) все утверждения А-Г верны
Задача 19.
В некоторых клетках таблицы 10 × 10 поставлены крестики так, что каждый из них — единственный либо в своей строке, либо в своём столбце. Какое наибольшее число крестиков может быть в такой таблице?
(А) 10
(Б) 15
(В) 18
(Г) 19
(Д) 99
Задача 20.
Разность корней квадратного уравнения x2 + bx + c = 0 — чётное число. Чему может равняться ордината вершины параболы y = x2 + bx + c ?
(А) −2
(Б) −3
(В) −4
(Г) −5
(Д) −6
Задача 21.
Винни-Пух пошёл в магазин за мёдом. Цена одного горшочка — 1 фунт, но при покупке n горшочков (n < 100) покупатель получает скидку n%. Когда Винни вернулся домой, Кристофер Робин посмотрел на его покупку и сказал: «Глупенький мой мишка! Ты ухитрился заплатить за мёд наибольшую возможную сумму денег!». Сколько фунтов заплатил Винни-Пух?
(А) 10
(Б) 15
(В) 20
(Г) 25
(Д) 50
Задача 22.
Числа от 1 до 120 выписаны в 15 строк, как показано на рисунке. В каком из столбцов (считая слева) сумма чисел самая большая?
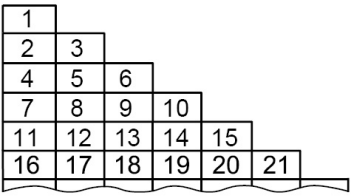
(А) 1
(Б) 4
(В) 5
(Г) 7
(Д) 13
Задача 23.
Про натуральные числа m и n известно, что каждое из них делится на числа 22 ⋅ 33 ⋅ 5 и 23 ⋅ 3, а каждое из чисел 25 ⋅ 37 ⋅ 53 и 24 ⋅ 36 ⋅ 52 делится на m и n. Чему равно наибольшее возможное отношение чисел m и n?
(А) 22 ⋅ 34 ⋅ 52
(Б) 2 ⋅ 33
(В) 22 ⋅ 33 ⋅ 52
(Г) 2 ⋅ 32 ⋅ 5
(Д) 2 ⋅ 33 ⋅ 5
Задача 24.
Правильный треугольник «катится» вокруг квадрата (см. рисунок ниже) Какую траекторию опишет отмеченная точка, прежде чем и она, и весь треугольник вернутся в исходное положение?

(А) 
(Б) 
(В) 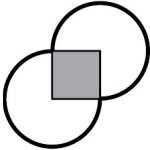
(Г) 
(Д) 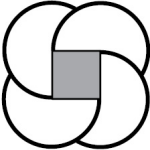
Задача 25.
Дробь 28/33 хотят представить в виде суммы нескольких дробей, числители которых равны 1. При каком наименьшем числе слагаемых это возможно?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 28
Задача 26.
На плоскости нарисовано несколько прямых. Рядом с каждой прямой написано число прямых, которые её пересекают. Среди написанных чисел имеется не менее четырёх различных, два из которых — это 6 и 7. Сколько прямых нарисовано?
(А) 9
(Б) 10
(В) 13
(Г) 15
(Д) невозможно определить
Задача 27.
В треугольнике длины сторон равны a, b и c, а угол, лежащий против стороны b, вдвое больше угла, лежащего против стороны a. Тогда обязательно
(А) a2 + c2 = b2
(Б) b2 + bc = a2
(В) c2 + ab = a2
(Г) a2 + ac = b2
(Д) каждое из соотношений А-Г может быть нарушено
Задача 28.
На рисунке ОА = 6 см, ОB = 4 см. Каково множество всех точек Р, лежащих в первой четверти, для которых площадь четырёхугольника PAOB равна 24 см2 ?
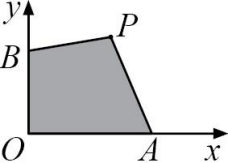
(А) 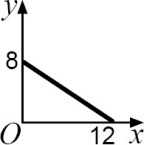
(Б) 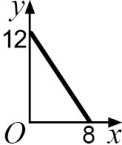
(В) 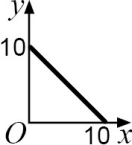
(Г) 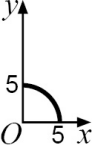
(Д) 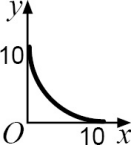
Задача 29.
Назовём тройку различных чисел, выбранных из множества {1, 2, 3, 4, 5, 6}, хорошей, если никакая пара чисел из этой тройки не имеет сумму 7. Коля перемножил числа в каждой хорошей тройке, а потом сложил полученные произведения. Какое число он получил?
(А) 72
(Б) 73
(В) 36
(Г) 37
(Д) 63
Задача 30.
Из 27 одинаковых маленьких кубиков сложили куб. Через середину его диагонали провели плоскость, перпендикулярную этой диагонали. Сколько маленьких кубиков пересекла эта плоскость?
(А) 17
(Б) 18
(В) 19
(Г) 20
(Д) 21

