Найдите сумму цифр числа, получаемого умножением 2018 на число, состоящее из 2018 единиц.

Решите ребус: БОЙ × 9 = ТУР (Одинаковым буквам соответствуют одинаковые цифры, разным — разные.)

Из шахматной доски вырезали клетчатый прямоугольник. Всегда ли оставшуюся часть доски можно разбить на доминошки? (Доминошка — фигура, состоящая из двух соседних по стороне клеток.)

В сидячем вагоне поезда стоят трёхместные скамейки для пассажиров: 20 рядов по 2 скамейки. Костя заметил, что на каждом ряду сидит 3 или 5 человек. Потом Костя подсчитал, на скольких скамейках сидит 3 человека и на скольких один человек. Найдите сумму Костиных чисел.

Найдите наибольшее число, такое, что если к нему прибавить сумму его цифр получится число 2018.

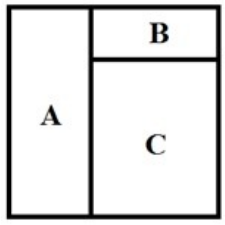
Витя составил из трёх прямоугольников квадрат с периметром 40 см. Периметр прямоугольника 𝐴 равен 28 см, а площадь прямоугольника 𝐵 — 18 см². Найдите площадь прямоугольника 𝐶. Ответ выразите в кв. см.

Из Новопетровска в Савельево Иван пошёл через лес со скоростью 4 км/ч, а Фёдор пошёл по дороге со скоростью 5 км/ч. Фёдор пришёл в Савельево на час позже и прошёл на 15 км больше, чем Иван. Найдите расстояние от Новопетровска до Савельева через лес.

Расставьте в клетках указанной фигурки числа от 5 до 14 так, чтобы суммы чисел во всех доминошках были разными (доминошка это прямоугольник, состоящий из двух клеток, соседних по стороне).