Каждый из детей одной семьи заявил, что у него ровно 4 брата (имеются в виду родные братья). При этом треть детей сказала правду, а остальные дети ошиблись. Сколько детей может быть в семье?

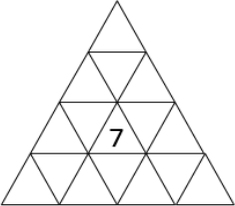
В треугольных ячейках фигурки записаны числа. Известно, что сумма чисел в фигурке из трёх треугольников, соединённых по стороне (любым образом повёрнутой), одна и та же. Костя выяснил, что в центре стоит число 7. Найдите сумму чисел во всех ячейках.

Дана доска 7 × 7. В середине доски стоит фишка. Костя и Никита играют в игру, по очереди передвигают фишку в соседнюю по стороне клетку. Но нельзя сразу делать ход, противоположный ходу соперника, то есть, если соперник сходил вниз, то сразу после этого хода нельзя ходить вверх, если соперник ходил влево, нельзя сразу после этого хода ходить вправо и т.д. Выигрывает тот, кто первым поставит фишку в клетку, в которой она уже была. Начинает Костя. Кто может всегда выигрывать в этой игре и как он должен для этого играть?

Каждый день Лёша съедает от 1 до 10 бутербродов. Лёша утверждает, что за все понедельники февраля 1919 года (аж век назад!) он съел на 37 бутербродов больше, чем за все субботы этого же месяца. Не ошибается ли Лёша?

Можно ли клетки квадрата 8 × 8 раскрасить ровно в 5 цветов так, чтобы выполнялись два условия: 1) клетки каждого цвета образовывали связную фигуру 2) в каждом столбце и в каждой строке были клетки ровно 3-х цветов? (Фигура называется связной, если из каждой клеточки фигуры можно добраться до любой другой, передвигаясь только в соседние по стороне клеточки.)

Маша загадала двузначное число и сообщила его мальчикам. Антон сказал, что в загаданном Машей числе есть цифра 7; Боря утверждает, что есть цифра 5; Вова заявил, что число чётное; Гоша уверяет, что число делится на 19; Дима сказал, что в загаданном числе цифры различны. Какое число загадала Маша, если известно, что четверо мальчиков сказали правду, а один мальчик ошибся? Требуется, конечно, найти все ответы и объяснить, что других ответов нет.

По кругу лежат пять одинаковых по весу и виду золотых монет. Фальшивомонетчик Иннокентий заменил из них какие-то (может быть всего одну, но хотя бы одну точно) фальшивыми, по виду точно такими же, но более лёгкими. При этом никакие две рядом лежащие монеты не стали фальшивыми. Как за два взвешивания на чашечных весах без гирь узнать, сколько монет фальшивых? (Фальшивые монеты весят одинаково.)

Никита раскладывал все свои дипломы по папкам. Когда он раскладывал дипломы по 13 штук в каждую папку он смог наполнить только 12 папок (возможно у него после этого остались дипломы, но следующую папку он заполнить не смог). Тогда Никита стал заново раскладывать все свои дипломы по 12 штук в папку, и он смог заполнить 14 папок (возможно у него и после этого остались дипломы, но следующую папку он заполнить не смог). Сколько у Никиты может быть дипломов?