Кикимора расставляет ловушки на квадратном болоте. Каждая ловушка имеет форму прямоугольника 2 × 3 клеточки. Кикимора хочет расставить семь ловушек так, чтобы они не соприкасались ни углами, ни сторонами. Какую наименьшую целую длину может иметь сторона болота?

Верочка считает четырёхзначное число милым, если его вторая цифра равна сумме первой и третьей, а его третья цифра равна сумме первой и четвёртой. Помогите Верочке найти самое маленькое милое число.

Илья Муромец выбирает на базаре новые доспехи и оружие. Он заметил, что два меча стоят столько же, сколько две кольчуги и один шлем вместе. При этом и кольчуга, и шлем дешевле меча.

Отметьте все верные утверждения:

1. три кольчуги стоят столько же, сколько два меча
2. шлем дешевле кольчуги
3. шлем дешевле, чем две кольчуги
4. меч дешевле, чем две кольчуги
5. ни одно из приведённых выше утверждений не является верным

В некотором месяце три понедельника пришлись на нечётные числа. Каким днём недели могло быть 15 число этого месяца? Найдите все подходящие варианты.

Как-то, отдыхая в Турции, ребята из кружка юных археологов нашли на берегу клинописные таблички с вавилонскими числами (Месопотамия, 2 тыс. до н.э.). На двух из них вавилонские числа были продублированы арабскими:

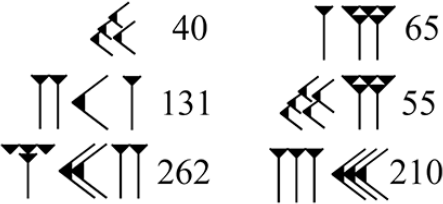
Помогите ребятам расшифровать числа на трёх табличках: