Задача 1.
Девять сундуков навалены в кучу:
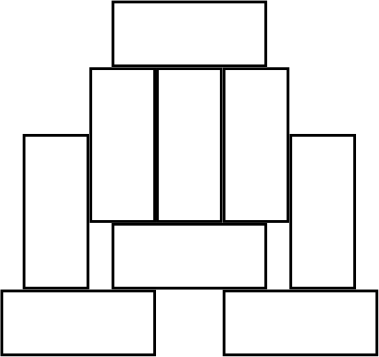
Покрась сундуки в три цвета так, чтобы:
-
касающиеся сундуки были покрашены в разные цвета
-
каждый из трёх цветов был использован ровно три раза
Задача 2.
Кенга и Крошка Ру прыгают по прямой:
- сначала Крошка Ру прыгает на четыре метра вперёд
- затем Кенга прыгает на шесть метров вперёд
- затем Крошка Ру прыгает на четыре метра вперёд
- затем Кенга прыгает на шесть метра вперёд
- и так далее: после каждого прыжка Кенги Крошка Ру прыгает на четыре метра, а после каждого прыжка Крошки Ру Кенга прыгает на шесть
- Сколько метров пропрыгала Кенга к тому моменту, как Крошка Ру впервые окажется не ближе 15 метров от точки своего старта?
-
Если предположить, что Кенга и Крошка Ру начали прыгать из одной точки в одном направлении, то сколько будет точек, в которых приземлялись и Кенга, и Крошка Ру, находящихся не далее 90 метров от точки старта?
Комментарий: Точку старта считать не нужно!
Задача 3.
Собрались Мо, Умо и Амо. Между ними завязался разговор:
- Первый сказал второму: «У тебя имя из трёх букв!»
- Второй сказал третьему: «У тебя имя из трёх букв!»
- Третий сказал первому: «Ты Умо!»
Только один из них сказал правду.
Кого как могли звать? Нужно указать все возможные варианты!
Задача 4.
В пропуски нужно вписать чис ла 1, 2, 3, 4 (в каждом из равенств каждое из этих чисел — по разу) так, чтобы равенства стали верными:
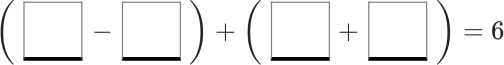
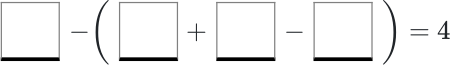

Задача 5.
Кок накрывает стол. Ему надо расположить шесть тарелок с крабами так, чтобы вдоль каждой из сторон стола было одинаковое количество крабов, но при этом были бы две стороны стола, вдоль которых стоит разное количество тарелок.
Вот план стола:
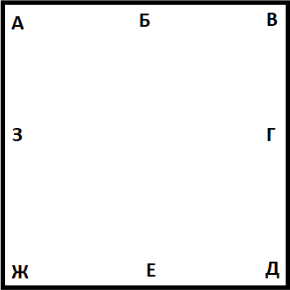
- В углы стола (А, В, Д, Ж) можно ставить не более одной тарелки.
- В неугловые области (Б, Г, Е, 3) можно ставить сколько угодно тарелок в ряд вдоль соответствующей стороны.
Помогите Коку расставить шесть тарелок:
- Тарелку с 1 крабом нужно поставить в область ...
- Тарелку с 2 крабами нужно поставить в область ...
- Тарелку с 3 крабами нужно поставить в область ...
- Тарелку с 3 крабами нужно поставить в область ...
- Тарелку с 4 крабами нужно поставить в область ...
- Тарелку с 4 крабами нужно поставить в область ...
Задача 6.
Робинзон ловил крабов. Пойманных крабов он сажал в корзину, ведро и ящик. Известно следующее:
- Робинзон поймал всего 13 крабов
- если пересадить краба из ящика в ведро, то в ящике станет столько же крабов, сколько было в корзине после того, как Робинзон поймал первых двух крабов
- среди остальных 11 крабов лишь один был посажен в корзину
Сколько куда крабов мог посадить Робинзон? Нужно найти все возможные варианты!
Задача 7.
Ефим составил из шести различных цифр, лишь две из которых отличаются на 1, три двузначных числа.
Разряды десятков этих чисел расположились в порядке убывания, а разряды единиц — в порядке возрастания.
Причём разряды десятков любых соседних чисел отличаются на столько же, на сколько отличаются разряды единиц любых соседних чисел.
Какие числа составил Ефим?

