Лесорубы умеют распиливать бревно на две части за 2 минуты. У них есть 5 брёвен длиной 10 метров. За какое время они распилят все бревна на чурбаки длиной 1 метр?

В Москве в январе было 10 ясных и безветренных дней. 15 дней был ветер и 12 дней шёл снег. Сколько дней была метель (то есть снег с ветром)?

Пачка бумаги в 500 листов имеет толщину 5 см. Напечатали книгу в 300 страниц. Какова толщина книги, если толщина обложки (с обеих сторон в сумме) 3 мм?

В восьмизначном числе 20102010 зачеркните три цифры так, чтобы получилось наименьшее из возможных пятизначное число.

Три одноклассника учатся в МГУ на механико-математическом факультете (мехмат), вычислительной математики и кибернетики (ВМиК) и химическом (химфак). Из трёх утверждений «Дима учится на химфаке», «Слава – не химик», «Лёша учится не на мехмате» только одно верное. Кто учится на химфаке?

Ковровая дорожка покрывает лестницу длиной 100 м и высотой 20 м. Какова длина дорожки?

Вода при замерзании увеличивается на одну одиннадцатую своего объёма. На какую часть своего объёма уменьшится лёд при обратном превращении в воду?

В августе одного из прошлых лет три воскресенья пришлись на чётные числа. Какой день недели был 9 августа этого года?

Расставьте знаки арифметических действий, чтобы получился верный пример: 1234567 = 2010.

Между деревнями Кошки и Мышки построили скоростную трассу. В целях безопасности над трассой построили стеклянное квадратное заграждение (см. рисунок).

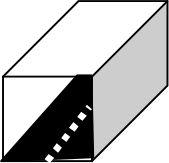
Мэр Кошек, проинспектировав сооружение, издал указ увеличить в два раза высоту заграждения. Во сколько раз увеличится расход стекла по сравнению с первоначальным?

Незнайке поручили покрасить клетчатые ставни 2×2 (см. рисунок) на окнах нового дома в Цветочном городе.

Незнайка красит каждую клетку в один из трёх цветов.

1. Сколько различных ставень он сможет получить?
2. Сколько различных ставень он сможет получить, если ставни можно красить не более чем в два цвета?
3. Сколько различных ставень он сможет получить, если ставни можно красить в два или три цвета, причём квадратики одного цвета не должны иметь общую сторону?