Задача 1.
У трёх братьев разное количество марок. Если старший даст среднему 1 марку, а средний даст младшему 3 марки, то у всех станет поровну. Сколько марок должен отдать старший младшему, чтобы у них двоих стало поровну?
Задача 2.
Расставьте в клеточки цифры 1, 2, 3, 4 так, чтобы в каждой строке и в каждом столбце присутствовали все 4 цифры и были выполнены указанные неравенства.
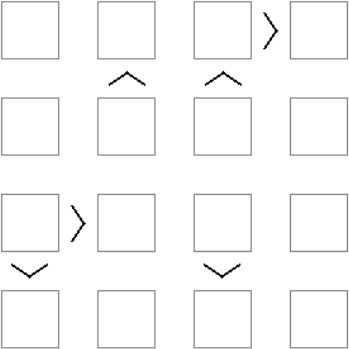
Задача 3.
Разрежьте квадрат 6×6 клеток на два равных 24-угольника. Резать можно только по линиям сетки.

Задача 4.
У Екатерины Михайловны была стопка из 10 блокнотов с обложками разных цветов: красной (К), белой (Б), чёрной (Ч), жёлтой (Ж), синей (С), фиолетовой (Ф), оранжевой (О), голубой (Г), розовой (Р) и зелёной (З). 10 детей встали в круг и ЕМ стала раздавать блокноты, каждому третьему, считая по кругу и пропуская тех, кому уже дала. В каком порядке лежали блокноты, если Егор получил жёлтый блокнот, и он был третьим, кто получил блокнот? Какие в результате все получили блокноты, изображено на рисунке.
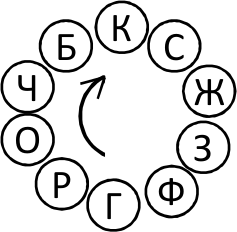
Комментарии: Если остаётся двое, то они считаются «первый, второй, третий», а затем выдаётся блокнот последнему. При счете ЕМ пропускает тех, кто уже получил блокнот.
Задача 5.
Найдите хотя бы одно решение ребуса (Одинаковым буквам соответствуют одинаковые цифры, разным – разные)
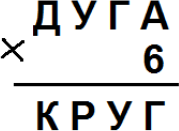
Задача 6.
Маша и Саша взяли с собой в школу по одинаковой пачке печенья и условились есть его на каждой перемене по 2 или 3 штуки. У Саши к концу четвёртого урока осталась только одно печенье, а у Маши к шестому уроку печенье закончилось. Сколько печенья в пачке?
Задача 7.
Встретил как-то Принц трёх ведуний и спросил про свою судьбу.
- Арта сказала: Будет у Принца супруга ленива. А победит он больше 100 Драконов.
- Бина: Нет-нет, победит Принц меньше 100 Драконов. Зато жена будет трудолюбива.
- Веда: Нет, жена, увы, будет ленивица. Зато хоть одного Дракона Принц точно победит.
Что ждёт Принца, если он знает, что одна из них вечно лжёт, другая всегда говорит правду, а третья сначала говорит правду, а потом лжёт?
Комментарий: Кто именно лжёт, а кто говорит правду, а кто попеременно – неизвестно.
Задача 8.
В ряд лежит 9 монет, известно, что среди них ровно три фальшивые, и они лежат подряд. Все фальшивые монеты весят одинаково и легче настоящих монет. Все настоящие монеты весят одинаково. Как за 2 взвешивания на чашечных весах без гирь найти все три фальшивые монеты?

