Задача 1.
Замените одинаковые буквы одинаковыми цифрами, а разные – разными так, чтобы получилось верное равенство:
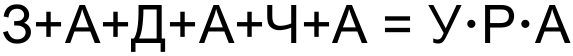
Задача 2.
На берегах очень извилистой речки живут Маша (М), Рома (Р) и Катя (К). Алиса раздобыла карту района, где живут ребята. Сможет ли она определить, кто живёт на одном берегу, а кто – на разных? Если да, укажите, кто живёт на одном берегу. Других водоемов в этом районе нет.

Река – непрерывная линия без самопересечений и отростков, но как конкретно она течёт – неизвестно.
Задача 3.
Если наливать воду в конструкцию на рисунке ниже, то первым заполнится сосуд А.
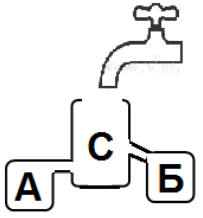
Какой сосуд заполнится первым, если открыть кран в конструкции на рисунке ниже?
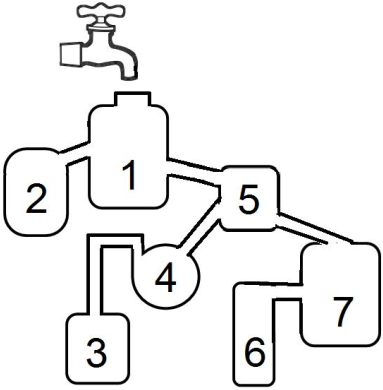
Задача 4.
От дома до школы у Клима два перехода со светофорами с зелёным и красным сигналом. От первого до второго перехода Клим идёт 2 минуты. Клим знает, что на каждом светофоре зелёный и красный горят равное время – по 2 минуты. Из дома до первого перехода идти 10 минут и от второго перехода до школы – тоже 10 минут. Однажды Клим вышел из дома в 8:00 и увидел, что на всех светофорах одновременно загорелся зелёный свет. Во сколько он придёт в школу, если не будет нарушать правила? (Клим переходит дорогу за 5 секунд)
Задача 5.
К наибольшему трёхзначному числу, делящемуся на 2, прибавили наименьшее трёхзначное число, не делящееся на 2. Чему равна сумма?
Задача 6.
В игровом автомате за одну игру нужно класть по 1 монетке одновременно в три круга, соединённых в малый треугольник. В кружках высвечивается число положенных в этот круг монет (в среднем круге сломался экран и числа не видно). Петя начал играть, когда в кругах были числа, как на рисунке слева, а закончил, как на рисунке справа. Сколько раз сыграл Петя?
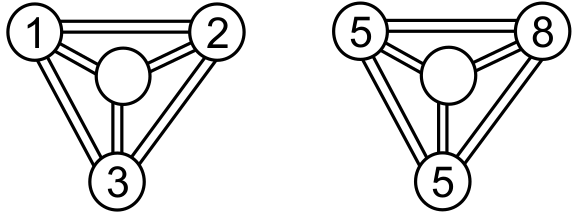
Комментарий: каждый раз три монетки нужно класть одновременно, при этом одну из них – обязательно в центральный круг, и две – в два любых круга по краям.
Задача 7.
Музей Хогвартса разбит на треугольные залы. Волшебный фонарь, установленный в одном зале, освещает все залы по трём направлениям (как на рисунке ниже).
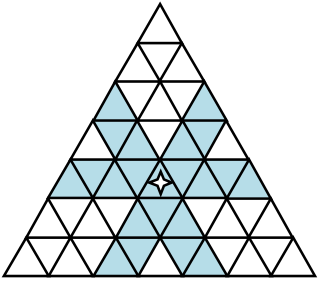
Если какой-то зал освещен с трёх сторон, он становится невидимым. Укажите на плане все невидимые залы.
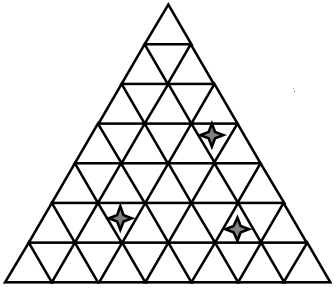
Задача 8.
Трое играли в домино. Каждый взял из набора по одной доминошке и сделал три заявления (каждый игрок сделал все три заявления, но в разном порядке):
- «На моей доминошке в сумме четыре точки».
- «У моей доминошки есть пустая половинка».
- «У моей доминошки одинаковые половинки».
Какие доминошки они взяли из набора, если каждый 2 раза сказал правду, а 1 раз ошибся?

