Задача 1.
Каждый из восьми кенгуру может перепрыгнуть на любую клетку квадратной таблицы 4 × 4. Им надо расположиться так, чтобы в каждой строчке и каждом столбце этой таблицы оказалось ровно по 2 кенгуру. Наименьшее число кенгуру, которым придётся для этого прыгнуть, равно:

(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 2.
Если к 2005 прибавить 2005 сотых, то получится:
(А) 2025,05
(Б) 2005,2005
(В) 2005,02005
(Г) 2007,05
(Д) 2205,5
Задача 3.
Муравей ползёт по поверхности кубика из точки А в точку В по пути, отмеченному стрелками. Чему равна длина этого пути, если ребро кубика равно 12 см?
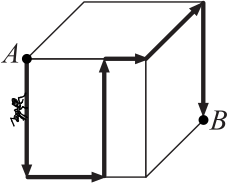
(А) 36 см
(Б) 48 см
(В) 50 см
(Г) 60 см
(Д) невозможно определить
Задача 4.
В треугольнике ABC угол A в три раза больше угла B и равен половине угла C. Тогда угол A равен:
(А) 30º
(Б) 36º
(В) 54º
(Г) 60º
(Д) 72º
Задача 5.
На картинке изображён план вольера для кенгуру в зоопарке. Все углы на плане — прямые. Какова площадь вольера?
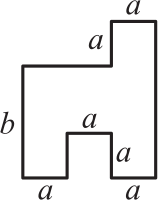
(А) 2ab + a(b − a)
(Б) 3a(a + b) − a2
(В) 3а(а + b)
(Г) 3a(b − a) + a2
(Д) 3ab
Задача 6.
Среди кошек, обитающих в лагере «Ласточка», три — пушистые, а две — полосатые. Какое наименьшее количество неполосатых пушистых кошек может быть в лагере?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 7.
Какое из следующих равенств означает, что m составляет 30% от k ?
(А) 10m − 7k = 0
(Б) 10m − 3k = 0
(В) 3m − 10k = 0
(Г) 7m − 10k = 0
(Д) 7m − 3k = 0
Задача 8.
На рисунке изображены квадрат и пять одинаковых кругов. Вершины квадрата расположены в центрах внешних кругов. Тогда отношение площади закрашенной части кругов к площади их незакрашенной части равно:
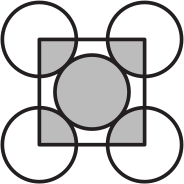
(А) 1 : 3
(Б) 1 : 4
(В) 2 : 5
(Г) 2 : 3
(Д) 5 : 4
Задача 9.
Если разделить 5050 на 2525, то получится:
(А) 2
(Б) 2525
(В) 225
(Г) 10025
(Д) 5025
Задача 10.
Сторож работает 4 дня, а на пятый день отдыхает. Он отдыхал в воскресенье и начал работу в понедельник. Сколько дней он проработает до того, как его отдых снова придётся на воскресенье?
(А) 4
(Б) 24
(В) 28
(Г) 32
(Д) 35
Задача 11.
С полуночи до полудня Кот Ученый рассказывает сказки, а с полудня до полуночи спит под дубом. На дубе том висит плакат: «Два часа назад Кот делал то же самое, что он будет делать через час». Сколько часов в сутки эта надпись верна?
(А) 6
(Б) 12
(В) 18
(Г) 3
(Д) 21
Задача 12.
Сумма пяти различных натуральных чисел равна 100. Каким может оказаться наибольшее из этих пяти чисел?
(А) 10
(Б) 20
(В) 90
(Г) 93
(Д) 96
Задача 13.
На рисунке изображена мишень, разделённая на 4 области. Очки за попадание в область обратно пропорциональны её площади. Сколько очков даёт попадание в область C, если попадание в область В даёт 10 очков?
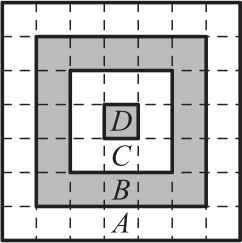
(А) 5
(Б) 8
(В) 16
(Г) 20
(Д) 24
Задача 14.
Вася придумал такой шифр: он заменил буквы Г, Е, К, Н, Р, У какими-то цифрами, идущими в возрастающем порядке. Потом при помощи этого шифра он зашифровал слово КЕНГУРУ. Какое наибольшее число могло у него получиться?
(А) 9876545
(Б) 9876543
(В) 7684969
(Г) 6574989
(Д) 5463878
Задача 15.
На чертеже изображены равносторонний треугольник и правильный пятиугольник. Найдите угол x.
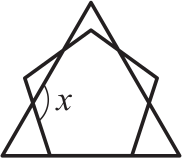
(А) 124º
(Б) 128º
(В) 132º
(Г) 136º
(Д) 140º
Задача 16.
Сколько различных имеется среди чисел 1 : (2 : (3 : 4)), (1 : 2) : (3 : 4), 1 : ((2 : 3) : 4), ((1 : 2) : 3) : 4, (1 : (2 : 3)) : 4?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 17.
На окружности с центром в точке O взяли точку A. Какую часть окружности составляют точки, которые ближе к O, чем к A?
(А) 3/4
(Б) 2/3
(В) 1/2
(Г) 5/6
(Д) ответ зависит от расположения точки A
Задача 18.
Жан-Кристоф продолжает изучать русский язык. Он собирается выписывать натуральные числа словами до тех пор, пока не напишет первое число, в записи которого участвуют все буквы слова «слово». Чему равна сумма цифр числа, на котором Жан-Кристоф остановится?
(А) 5
(Б) 8
(В) 9
(Г) 10
(Д) 30
Задача 19.
Назовем длиной натурального числа n количество сомножителей в разложении n на простые множители. Например, длина числа 90 равна 4, так как 90 = 2 ⋅ 3 ⋅ 3 ⋅ 5. Сколько нечётных чисел, меньших 100, имеют длину 3?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 20.
Игральный кубик, развёртка которого изображена на рисунке, поставили на клетку М, прокатили по маршруту МON и нашли сумму всех восьми цифр, которые побывали сверху. Сколько получилось?
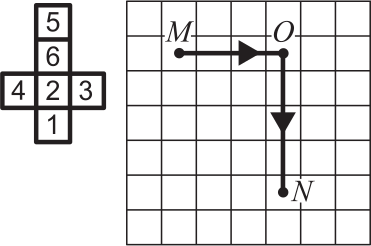
(А) 42
(Б) 35
(В) 28
(Г) 21
(Д) невозможно определить
Задача 21.
Числа a и b таковы, что 4 ≤ a ≤ 6, 1 ≤ b ≤ 2 . Какое из следующих чисел обязательно меньше 9?
(А) 2a − 3b
(Б) a + 2b
(В) 3a − b
(Г) 8b − 2a
(Д) 13b − a
Задача 22.
Два прямоугольника ABCD и DBEF расположены так, как показано на чертеже. Какова площадь прямоугольника DBEF?
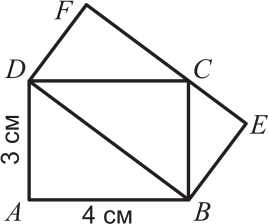
(А) 10 см2
(Б) 12 см2
(В) 13 см2
(Г) 14 см2
(Д) 15 см2
Задача 23.
Сколько существует двузначных чисел, которые при перестановке цифр увеличиваются не менее, чем в три раза?
(А) 5
(Б) 6
(В) 10
(Г) 15
(Д) 33
Задача 24.
Гусеница выползла из домика в полдень и ползёт по лугу, поворачивая через каждый час на 90º направо или налево. За первый час она проползла 1 м, за второй час — 2 м, и т. д. На каком наименьшем расстоянии от домика она могла оказаться в 9 часов вечера?
(А) 0 м
(Б) 1 м
(В) 2 м
(Г) 1,5 м
(Д) 0,5 м
Задача 25.
Сколько четырёхугольников с вершинами в отмеченных точках изображено на картинке?
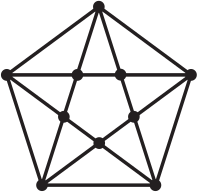
(А) 15
(Б) 20
(В) 25
(Г) 30
(Д) другой ответ
Задача 26.
На стороне BC равнобедренного треугольника ABC с основанием AC нашлась такая точка M, что ∠MCA − ∠MAB = ∠B. Что можно утверждать об этом треугольнике?
(А) он равносторонний
(Б) один из его углов прямой
(В) боковая сторона больше основания
(Г) угол при вершине B — тупой
(Д) основание больше боковой стороны
Задача 27.
Шерлок Холмс и доктор Ватсон ехали из Лондона в Плимут. Когда они прибыли в Плимут, доктор Ватсон спросил: «Холмс, а сколько времени мы были в пути?». «Не знаю, – ответил Холмс, – но я заметил, что в момент, когда мы отправлялись, и сейчас, когда мы прибыли, угол между часовой и минутной стрелками моих часов был прямым». Расстояние от Лондона до Плимута равно 120 км. Какой может быть скорость поезда?
(А) 120 км/ч
(Б) 110 км/ч
(В) 100 км/ч
(Г) 60 км/ч
(Д) никакой из перечисленных
Задача 28.
Сколько существует треугольников со сторонами 5 см и 6 см, один из углов которого равен 20º?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 29.
По определению, n! = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n. Какой сомножитель нужно вычеркнуть из произведения 1! ⋅ 2! ⋅ 3! ⋅ 4! ⋅ …⋅ 20!, чтобы оставшееся произведение стало квадратом некоторого натурального числа?
(А) 20!
(Б) 19!
(В) 10!
(Г) 5!
(Д) это невозможно
Задача 30.
Двое играют в такую игру: они по очереди закрашивают прямоугольники 1 × 2 на доске, изображённой на рисунке.

Клетки доски запрещается красить дважды. Проигрывает тот, кто не может сделать хода. Какой из ходов гарантирует первому игроку победу?
(А) 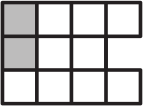
(Б) 
(В) 
(Г) 
(Д) 

