Задача 1.
Кенгуру способен прыгнуть в длину на 1 сантикилометр. Сколько метров составляет длина такого прыжка?
(А) 1
(Б) 5
(В) 10
(Г) 50
(Д) 100
Задача 2.
Часы лежат на столе циферблатом вверх. Минутная стрелка сейчас указывает на северо-восток. Через сколько минут она укажет на северо-запад?
(А) 45
(Б) 40
(В) 30
(Г) 20
(Д) 15
Задача 3.
В каком из следующих выражений при замене цифры восемь на любую другую цифру результат не изменится?
(А) (8 + 8) : 8 + 8
(Б) 8 × (8 + 8) : 8
(В) 8 + 8 − 8 + 8
(Г) (8 + 8 − 8) × 8
(Д) (8 + 8 − 8) : 8
Задача 4.
Веня сложил лист бумаги пополам (как показано на рисунке) и сделал два прямых разреза ножницами. Затем он развернул лист. Какую фигуру он не мог при этом получить?
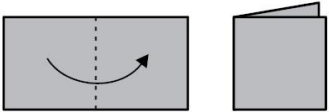
(А) 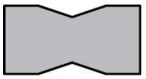
(Б) 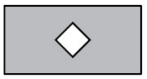
(В) 
(Г) 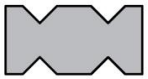
(Д) 
Задача 5.
Натуральные числа x и y таковы, что 12x и 18y являются точными квадратами. Чему равно наименьшее возможное значение суммы x + y ?
(А) 2
(Б) 5
(В) 7
(Г) 13
(Д) 30
Задача 6.
На рисунке изображена схема дорожек в парке. Каждая из этих девяти дорожек имеет длину 100 м. Аня хочет прогуляться из точки A в точку B, не проходя ни по какой дорожке дважды. Какова наибольшая длина такой прогулки?
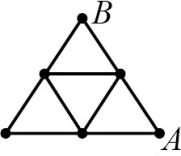
(А) 900 м
(Б) 800 м
(В) 700 м
(Г) 600 м
(Д) 400 м
Задача 7.
Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 50° и 60°?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) ни одного
Задача 8.
Числа a, b, c и d таковы, что (a + b)2 + (c + d)2 = 2(a2 + b2 + c2 + d2). Тогда обязательно
(А) a = c и b = d
(Б) a = b и c = d
(В) a = d и b = c
(Г) a = b = c = d
(Д) a + b = c + d
Задача 9.
На какое наименьшее число треугольников можно разрезать фигурку кенгуру на рисунке?
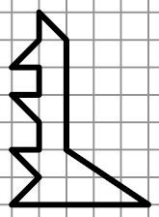
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 10.
Чему равен куб периметра квадрата площади 4?
(А) 4
(Б) 8
(В) 64
(Г) 512
(Д) 1024
Задача 11.
Барбара заполняет пустые клетки таблицы (см. рисунок). Она хочет, чтобы сумма трёх верхних чисел была равна 100, сумма трёх средних чисел была равна 200, а сумма трёх нижних чисел была равна 300. Какое число она должна поставить в среднюю клетку?

(А) 50
(Б) 60
(В) 70
(Г) 75
(Д) 100
Задача 12.
Есть четыре карточки с надписями: «делится на 7», «простое», «нечётное» и «больше 100». На другой стороне карточек написаны числа 2, 5, 7 и 12. Для любой карточки число, написанное на ней, не обладает свойством, написанным на её обороте. Какое число написано на карточке с надписью «делится на 7»?
(А) 2
(Б) 5
(В) 7
(Г) 12
(Д) невозможно определить
Задача 13.
В пятиконечной звезде даны три угла (см. рисунок). Известно, что AB = BC. Чему равен угол x?
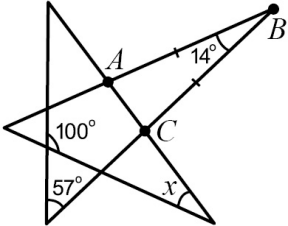
(А) 35°
(Б) 42°
(В) 54°
(Г) 65°
(Д) 109°
Задача 14.
Миша выбирает несколько чисел из набора 1, 2, …, 10 так, чтобы ни одно выбранное число не было в два раза больше другого. Какова наибольшая возможная сумма таких чисел?
(А) 37
(Б) 39
(В) 41
(Г) 42
(Д) 45
Задача 15.
Число x положительно, а число y отрицательно. Что обязательно произойдёт, если число x увеличится, а число y уменьшится?
(А) x + y уменьшится
(Б) xy увеличится
(В) x/y уменьшится
(Г) y/x уменьшится
(Д) x − y увеличится
Задача 16.
За один шаг робот может либо умножить данное число на 2, либо поделить его на 3, либо возвести его в квадрат. За какое наименьшее число шагов этот робот может превратить число 45 в число 200?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) 3
Задача 17.
Игральный кубик прокатили по клетчатой дорожке (см. рисунок). В каких двух позициях верхняя грань кубика была одна и та же?
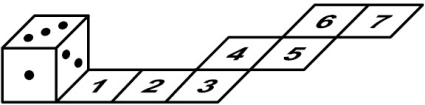
(А) 1 и 7
(Б) 2 и 6
(В) 1 и 5
(Г) 2 и 7
(Д) 1 и 6
Задача 18.
У Пети и Коли были две одинаковые прямоугольные карточки. Каждый мальчик разрезал свою карточку на два прямоугольника. Сумма периметров прямоугольников, которые получились у Пети, равна 40, а у Коли — 50. Чему равен периметр исходной карточки?
(А) 20
(Б) 24
(В) 30
(Г) 36
(Д) так разрезать карточки невозможно
Задача 19.
В одном городе 20% семей, имеющих кошек, имеют также и собак, 25% семей, имеющих собак, имеют также и кошек, а 20% всех семей не имеют ни кошек, ни собак. Сколько семей в этом городе имеют и кошек, и собак?
(А) 50%
(Б) 25%
(В) 20%
(Г) 10 %
(Д) 5%
Задача 20.
Какое число надо удалить из набора 1, 2, 3, …, 9, чтобы наименьшее общее кратное оставшихся чисел было самым маленьким из возможных?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 21.
Числа 1, 2, …, 12 расставлены по кругу так, что любые два соседних числа различаются либо на 2, либо на 3. Какие два числа стоят рядом?
(А) 6 и 8
(Б) 3 и 5
(В) 7 и 9
(Г) 5 и 8
(Д) так расставить числа нельзя
Задача 22.
Все углы шестиугольника ABCDEF равны 120°. Известно, что AB = 3, BC = 4, CD = 5 и EF = 1. Найдите DE + AF.
(А) 8
(Б) 10
(В) 13
(Г) 14
(Д) 15
Задача 23.
Натуральные числа a и b таковы, что a + b = 125. Какое из равенств А-Г возможно при некотором натуральном k?
(А) 2a ⋅ 3b = 12k
(Б) 2a ⋅ 3b = 18k
(В) 2a ⋅ 3b = 36k
(Г) 2a ⋅ 3b = 72k
(Д) никакое из перечисленных
Задача 24.
В квадрате 3 × 3 расставлены числа так, что произведение чисел в каждой строке и в каждом столбце равно 1, а произведение чисел в каждом квадрате 2 × 2 равно 2. Какое число стоит в центральной клетке?
(А) 16
(Б) 8
(В) 4
(Г) 1/4
(Д) 1/8
Задача 25.
Передние колёса роликовых коньков приходят в негодность после 300 км пробега, а задние — после 500 км. Диме подарили новые роликовые коньки. После скольких километров пробега ему нужно поменять местами задние и передние колёса, чтобы они прослужили одинаково долго?
(А) 212,5 км
(Б) 200 км
(В) 187,5 км
(Г) 175 км
(Д) 162,5 км
Задача 26.
Равносторонний треугольник поворачивают относительно центра на 3°, потом на 9°, на 27°, и т.д. (на n-м шаге его поворачивают на 3n градусов). Сколько всего разных положений будет занимать треугольник?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 360
Задача 27.
Произведение всех натуральных делителей числа n (включая и само n) оканчивается ровно на 15 нулей. На какое наибольшее количество нулей может оканчиваться число n?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 28.
Бумажный прямоугольник ABCD со сторонами AB = 3 и BC = 9 перегнули так, что вершина C совпала с вершиной A (см. рисунок). Чему равна площадь закрашенного пятиугольника?
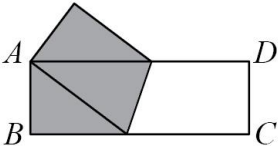
(А) 18
(Б) 19,5
(В) 20,5
(Г) 21
(Д) 27
Задача 29.
Назовем семизначное число счастливым, если у него сумма цифр, стоящих на чётных местах, равна сумме остальных цифр. Число может оказаться счастливым, если
(А) его цифры увеличиваются слева направо
(Б) его цифры уменьшаются слева направо
(В) на всех нечётных местах стоит цифра 7
(Г) его средняя цифра равна 1, а остальные симметричны относительно неё
(Д) его средняя цифра равна 2, а остальные симметричны относительно неё
Задача 30.
У Васи много квадратов со стороной 1 и правильных пятиугольников со стороной 1. Он хочет сложить из них «кольцо», прикладывая имеющиеся многоугольники друг к другу сторонами так, чтобы квадраты и пятиугольники чередовались. При этом образовавшийся внутри кольца многоугольник должен быть выпуклым. Какое наименьшее количество фигур ему придётся использовать?
(А) 8
(Б) 10
(В) 12
(Г) 16
(Д) 20

