9 гномов поселились в 9 комнатах, расположенных в виде квадрата 3 × 3. Как только они поселились, каждый пожал руки своим соседям (соседи по стороне). На второй день они поселились по-другому, и каждый пожал руки своим новым соседям. На третий день они снова переселились, и снова, каждый пожал руки каждому своему соседу. Докажите, что после трёх дней найдутся два гномика, которые не жали руки друг другу.

Остап Бендер организовал раздачу слонов населению. Явилось двадцать человек. Остап построил их по кругу, дал первому одного слона, его соседу слева — тоже одного слона, затем одного человека пропустил, следующему дал одного слона, пропустил двоих, следующему дал двух слонов, пропустил троих, следующему дал трёх слонов и т. д., пока не раздал всех 2018 имеющихся у него слонов. Скольким желающим не досталось ни одного слона?

В классе 20 человек. Никакие три девочки не дружат с одинаковым числом мальчиков. Какое наибольшее количество девочек может быть в классе?

В однокруговом футбольном турнире участвуют пятнадцать команд. Могло ли после окончания турнира оказаться, что у каждой команды количество ничьих равно количеству поражений?

Есть 30 камней различных весов и специальные весы. На эти весы можно класть только ровно по 10 камней на каждую чашку, тогда весы информируют, на какой чашке груз больше. Как с помощью этих весов найти пару камней, про которые точно будет известно, какой из них тяжелее?

Калькулятор «Зеленый остров» умеет выполнять две операции: вычитать из числа единицу или записывать цифры числа в обратном порядке, причём вторая операция разрешена только тогда, когда последняя цифра числа не равна нулю. За какое наименьшее число операций можно с помощью «Зелёный остров» из числа 100 получить число 1?

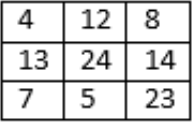
В таблице 3 × 3 расставлены числа (см. рисунок). Дима и Вера вычеркнули по 4 числа, причём сумма чисел, которые вычеркнула Вера в 3 раза больше суммы чисел, вычеркнутых Димой. Какое число осталось невычеркнутым?

В царстве гномов есть столица и города. Из столицы выходит одна дорога, из остальных городов выходит по три дороги. Одна дорога соединяет два разных города. Король гномов хочет распределить дороги между пожарными, милиционерами и докторами так, чтобы на каждой дороге дежурил ровно один человек и чтобы на трёх дорогах из одного города дежурили три разных специалиста. Докажите, что у Короля ничего не получится.