Задача 1.
Тихон вытащил из полного комплекта домино все доминошки, сумма точек на которых — чётное число. Можно ли из оставшихся доминошек сложить цепочку по правилам игры? (К единице прикладывается единица, к двойке двойка, к тройке тройка и так далее.)
Задача 2.
Во всех клетках таблицы стоят нули. Катя несколько раз выбирает квадрат 2 × 2 и увеличивает на 1 все числа, стоящие в нём. Какое число написано в центре таблицы (см. рисунок), если известны числа только в четырёх клетках исходной таблицы?
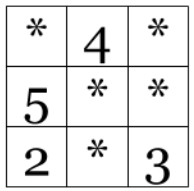
Задача 3.
У Егора есть 5 алмазов, разных по массе. У него есть прибор, в который можно положить 2, 3 или 4 алмаза, и тогда прибор покажет на самый тяжёлый из них. Егор хочет найти алмаз, средний по весу. Как ему это сделать, использовав прибор три раза?
Задача 4.
За каждую полученную в школе «пятёрку» Пете разрешалось одну минуту покрутить спиннер. При этом за каждую десятую «пятёрку» добавлялась ещё одна минута, а за каждую сотую добавлялось ещё пять минут (т.е. за сотую «пятёрку» Петя получал стандартную минуту, плюс дополнительную «за каждую десятую» и плюс пять дополнительных «за каждую сотую»). В течении учебного года Петя крутил спиннер 3 часа 20 минут. Сколько «пятёрок» получил в течении этого учебного года?
Задача 5.
Из клетчатого квадрата 16 × 16 вырезали по сторонам клеток прямоугольник из 70 клеток. Чему равен периметр этого прямоугольника, если сторона клетки равна 1?
Задача 6.
У Арнольда есть 27 пакетов с сахаром весом 1 кг, 2 кг, . . . , 27 кг. Он их разложил на кучки, в каждой из которых самый тяжёлый пакет весит столько же, сколько и все остальные вместе. Найдите число кучек.

