Задача 1.
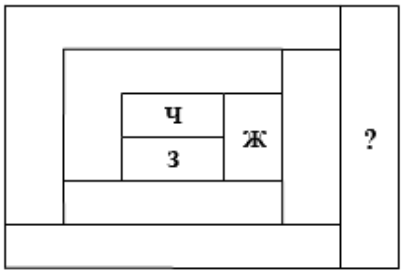
Каждую область на схеме ниже красят одним из четырёх цветов: чёрным (Ч), зелёным (З), жёлтым (Ж) или синим (С). При этом две области, имеющие общий отрезок границы, нельзя красить в один и тот же цвет. При условии, что центральные области окрашены так, как это показано на рисунке, в какой цвет может быть окрашена крайняя правая область?
Задача 2.
«Динамо» сыграло 6 матчей: 1 матч команда выиграла, 2 свела вничью и 3 проиграла. Всего во всех играх динамовцы забили 5 голов и пропустили 3 мяча. С каким счётом мог завершиться матч, в котором «Динамо» победило?
Задача 3.
Найти восемь последовательных целых чисел так, чтобы сумма первых пяти равнялась сумме трёх последних.
Задача 4.
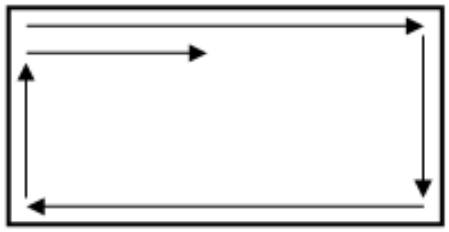
На клетчатом листе нарисован прямоугольник (100 строк и 200 столбцов). Клетки прямоугольника постепенно закрашивают: начинают с левой верхней клетки и идут вдоль спирали по часовой стрелке, как это показано на рисунке ниже: дойдя до края по ещё не закрашенным клеткам, каждый раз возвращаются направо. Какая клетка прямоугольника будет закрашена последней?
Задача 5.
У Оли есть 30 гирь. Все гири весят разное целое число килограмм, не более 60 кг, а общий вес — чётное число килограмм. Оля выяснила, что её гири нельзя разделить на 2 равные по массе части. Могло ли такое быть?
Задача 6.
В вазе лежат конфеты. Один школьник может съесть не более семи конфет. Чтобы съесть все конфеты из вазы необходимо четыре школьника. Когда в вазу положили ещё 11 конфет, пришлось звать на помощь ещё двух школьников. Какое наименьшее количество конфет могло быть в вазе первоначально?

