Задача 1.
Три стрелка Пётр, Евгений и Семён сделали по шесть выстрелов в одну и ту же мишень и выбили по одинаковому количеству очков. Известно, что Пётр за первые три выстрела выбил 43 очка, а Евгений первым выстрелом выбил 3 очка. Известно, что в 50 очков было одно попадание, в 25 — два, в 20 — три, в 10 — три, в 5 — два, в 3 — два, в 2 — два, в 1 — три. Кто наибольшее количество раз выбил 10 очков?
Задача 2.
Леночка составляет трёхзначное число. Сначала она записывает цифры в разряды единиц и десятков. Если сумма этих двух цифра меньше или равна 5, то Леночка записывает в разряд сотен чётную цифру, в ином случае — нечётную. Сколько трёхзначных чисел может получиться у Леночки?
Задача 3.
Можно ли квадратную сетку 3 × 3 собрать из трёх ломаных? (Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами. Никакие две ломаные не должны иметь общих отрезков.)
Задача 4.
На уроке математики учитель написал на доске 6 различных цифр. Мальчик Серёжа выбрал три цифры и составил из них самое большое число, которое можно было составить из этих трёх цифр. Мальчик Костя из оставшихся трёх цифр составил наименьшее число, которое можно было составить из этих трёх цифр. Сумма чисел, которые составили мальчики, оказалась равна 499. Какие числа написали составили мальчики?
Задача 5.
Есть три монеты. Одна из них фальшивая. Вася и Петя (один рыцарь, другой лжец, кто именно кто — неизвестно) знают, какая монета фальшивая. Разрешается выбрать одну или две монеты и спросить у Васи или у Пети, есть ли среди них фальшивая. Вася и Петя отвечают только «да» или «нет», рыцари всегда говорят правду, лжецы всегда лгут. Как за 2 вопроса определить хотя бы одну настоящую монету?
Задача 6.
Натуральные числа от 1 до 40 000 выписаны по порядку: 1234567891011 . . . 40000. Сколько раз в этой последовательности цифр встречается комбинация 2018 (именно в этом порядке)?
Задача 7.
Можно ли выложить прямоугольник 10 × 9 используя фигурки из набора, изображённого ниже? Фигурки можно поворачивать и переворачивать.
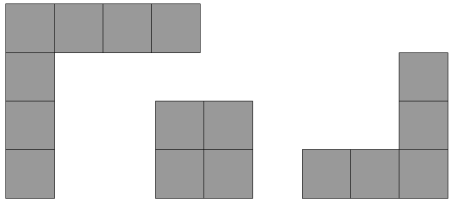
Задача 8.
В 10 мешках находится ровно 1000 орехов, при этом в каждом мешке их разное количество. В какой-то момент выбирается мешочек, в котором максимум орехов, берутся из него 9 орехов и раскладывается по 1 в каждый из других мешочков. Такая процедура повторяется пока не наступит момент, когда по крайней мере в двух мешочках количество орехов станет одинаковым. Обязательно ли процедура закончится через конечное количество шагов?

