В некотором месяце некоторого года ровно 5 пятниц. При этом первый и последний день этого месяца — не пятницы. Каким днём недели является 12-е число месяца?

За круглый стол рассадили несколько человек так, что между соседними людьми расстояния одинаковые. Одному из них дали табличку с номером 1 и дальше по часовой стрелке раздали всем таблички с номерами 2, 3 и т. д.

Человек с табличкой с номером 31 заметил, что от него до человека с табличкой с номером 7 такое же расстояние, как и до человека с табличкой с номером 14. Сколько всего людей сели за стол?

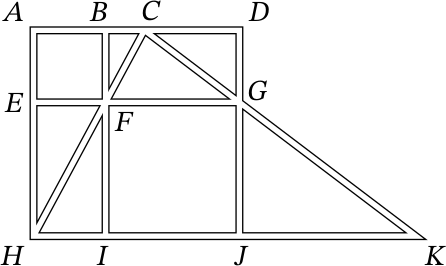
На рисунке изображён план системы дорог некоторого города. В этом городе 8 прямых улиц, а 11 перекрёстков названы латинскими буквами 𝐴, 𝐵, 𝐶, …, 𝐽, 𝐾.

На некоторые три перекрёстка надо поставить по полицейскому так, чтобы на каждой из 8 улиц стоял хотя бы один полицейский. На какие именно три перекрёстка надо поставить полицейских? Достаточно указать хотя бы один подходящий вариант расположения.

Комментарий: Все улицы направлены вдоль прямых линий. Всего 8 улиц:

• Горизонтальные улицы: 𝐴-𝐵-𝐶-𝐷, 𝐸-𝐹-𝐺, 𝐻-𝐼-𝐽-𝐾.
• Вертикальные улицы: 𝐴-𝐸-𝐻, 𝐵-𝐹-𝐼, 𝐷-𝐺-𝐽.
• Наклонные улицы: 𝐻-𝐹-𝐶, 𝐶-𝐺-𝐾.

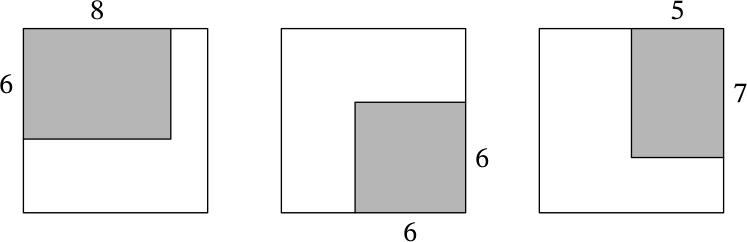
Директор школы, завхоз и родительский комитет, не договорившись друг с другом, купили по ковру для школьного актового зала размером 10 × 10. Подумав, что же делать, они решили положить все три ковра так, как показано на картинке: первый ковёр 6 × 8 — в один угол, второй ковёр 6 × 6 — в противоположный угол и третий ковёр 5 × 7 — в один из оставшихся углов (все размеры указаны в метрах).

Найдите площадь части зала, накрытой коврами в три слоя (ответ дайте в квадратных метрах).

На кружки по математике записалось несколько школьников. Их хотят распределить по группам равномерно — таким образом, чтобы количество учеников в любых двух группах отличалось не более чем на 1.

В результате такого равномерного деления получилось 6 групп, среди которых ровно 4 группы по 13 учеников. Сколько всего могло быть школьников? Укажите все возможные варианты.

Несколько камней разложены в 5 кучек. Известно, что

• в пятой кучке камней в шесть раз больше, чем в третьей;
• во второй кучке камней вдвое больше, чем в третьей и пятой вместе взятых;

• в первой кучке камней втрое меньше, чем в пятой, и на 10 меньше, чем в четвёртой;

• в четвёртой кучке камней в два раза меньше, чем во второй.

Сколько всего суммарно камней в этих пяти кучках?

После чемпионата мира по хоккею три журналиста написали статью о сборной Германии — каждый для своей газеты.

• Первый написал: «Сборная Германии за весь чемпионат забила больше 10, но меньше 17 шайб».

• Второй: «Сборная Германии забила больше 11, но меньше 18 шайб за весь чемпионат».

• Третий: «Сборная Германии забила нечётное количество шайб за весь чемпионат».

В итоге оказалось, что правы были только два журналиста. Сколько шайб могла забить сборная Германии на чемпионате? Укажите все возможные варианты.

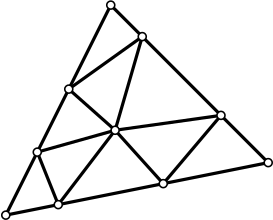
Внутри большого треугольника периметра 120 провели несколько отрезков, которые разделили его на девять меньших треугольников, как показано на рисунке. Оказалось, что периметры всех девяти маленьких треугольников равны между собой. Чему они могут быть равны? Укажите все возможные варианты.

Комментарий: Периметр фигуры — сумма длин всех её сторон.