Задача 1.
Значение выражения $\displaystyle \left(1 + \frac{1}{2}\right)⋅\left(1 + \frac{1}{3}\right)⋅\ldots..⋅\left(1 + \frac{1}{2003}\right)$ равно:
(А) 2004
(Б) 2003
(В) 2002
(Г) 1002
(Д) 1001
Задача 2.
Круглая клумба в нашем саду имеет диаметр 1,2 м. В соседнем саду круглая клумба имеет площадь в 4 раза больше нашей. Каков её диаметр?
(А) 2,4 м
(Б) 3,6 м
(В) 4,8 м
(Г) 6,4 м
(Д) 9,6 м
Задача 3.
Когда бочка пуста на 30%, она содержит на 30 литров больше мёда, чем когда она полна на 30%. Сколько литров мёда в полной бочке?
(А) 60
(Б) 75
(В) 90
(Г) 100
(Д) 120
Задача 4.
Маша нарисовала на экране компьютера букву, а потом нажала последовательно три кнопки: «повернуть на 90° по часовой стрелке», «заменить на зеркальное изображение» и «повернуть на 180°». Какую картинку она увидит?
(А) 
(Б) 
(В) 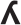
(Г) 
(Д) 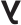
Задача 5.
Если сумма углов треугольника равна $a$, то квадрат угла квадрата равен
(А) $\displaystyle \frac{a}{2}$
(Б) $\displaystyle \frac{a^2}{2}$
(В) $\displaystyle \frac{a^2}{4}$
(Г) $\displaystyle \frac{a}{4}$
(Д) $a^2$
Задача 6.
Чему равна сумма $|2 − \sqrt{5}| + |3 − \sqrt{5}|$ ?
(А) $5 − 2\sqrt{5}$
(Б) $2\sqrt{5} − 5$
(В) $2\sqrt{5} + 5$
(Г) 1
(Д) 5
Задача 7.
Ребро куба равно 1. Муха ползает по рёбрам этого куба, не проходя по одному ребру дважды (но, возможно, проходя несколько раз через одну вершину). Какой самый длинный путь она может проползти?
(А) 6
(Б) 8
(В) 9
(Г) 10
(Д) 12
Задача 8.
Вася составляет всевозможные дроби вида $\displaystyle \frac{a}{b}$, беря $a$ из набора {68, 60, 54, 51, 48, 45}, а $b$ — из набора {20, 17, 15, 12}. Каково отношение самой большой и самой маленькой таких дробей?
(А) $\displaystyle \frac{68}{27}$
(Б) $\displaystyle \frac{68}{3}$
(В) $\displaystyle \frac{51}{4}$
(Г) $\displaystyle \frac{17}{12}$
(Д) $\displaystyle \frac{17}{9}$
Задача 9.
Из четырёх деталей, каждая из которых состоит из четырёх маленьких кубиков, сложили прямоугольный параллелепипед, показанный на рисунке. Каждая деталь окрашена в свой цвет. Как выглядит белая деталь?
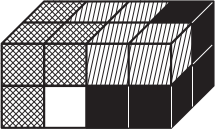
(А) 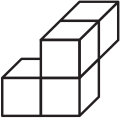
(Б) 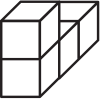
(В) 
(Г) 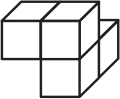
(Д) 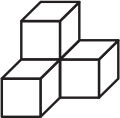
Задача 10.
Сколькими способами можно записать число 2003 в виде суммы а + b, где а и b — простые числа и а < b?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) более 3
Задача 11.
В прямоугольнике ABCD площади 1 точки P, Q, R и S — середины сторон, а точка Т — середина отрезка RS. Какова площадь треугольника PQT ?
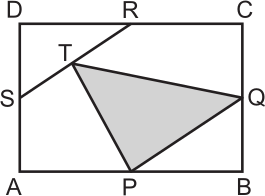
(А) $\displaystyle \frac{5}{16}$
(Б) $\displaystyle \frac{1}{4}$
(В) $\displaystyle \frac{1}{5}$
(Г) $\displaystyle \frac{1}{6}$
(Д) $\displaystyle \frac{3}{8}$
Задача 12.
На координатной плоскости даны прямые у = 2 + х и у = 1 – х. Они разбивают плоскость на 4 части. Занумеруем эти части против часовой стрелки, начиная с той, в которой лежит начало координат. В какой из частей лежит точка А (−2003, 2003)?
(А) в первой
(Б) во второй
(В) в третьей
(Г) в четвёртой
(Д) на одной из данных прямых
Задача 13.
Сколькими способами числа 2, 4, 8, 16, 32, 64, 128, 256 можно разбить на пары, чтобы отношения чисел во всех парах были одинаковыми?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) более 3
Задача 14.
Костя Сергеев из 9А класса и 8 его друзей из той же школы отправились в поход. Оказалось, что среди любых четырёх из этих туристов обязательно есть одноклассники, а среди любых пяти — не больше, чем три одноклассника. Сколько учеников 9А класса пошли в поход?
(А) 2
(Б) 3
(В) 4
(Г) 1
(Д) невозможно определить
Задача 15.
Центры четырёх полукругов, изображённых на рисунке, лежат на серединах сторон квадрата. Радиусы этих полукругов равны 1. Каков радиус окружности, которая касается этих четырёх полукругов?
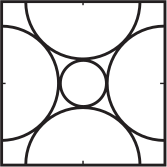
(А) $\sqrt{2} − 1$
(Б) $\displaystyle \frac{1}{2}π − 1$
(В) $\sqrt{3} − 1$
(Г) $2\sqrt{2} − 2$
(Д) $2 − \sqrt{2}$
Задача 16.
Будем называть старшим делителем числа n самый большой из его делителей, отличных от самого числа n. Аналогично, младший делитель числа n — это самый маленький его натуральный делитель, отличный от 1. Сколько существует таких натуральных чисел n, для которых старший делитель в 18 раз больше младшего?
(А) 0
(Б) 1
(В) 2
(Г) бесконечно много
(Д) другой ответ
Задача 17.
Правильный шестиугольник и правильный треугольник имеют одинаковые периметры. Каково отношение их площадей?
(А) 1
(Б) 3/2
(В) 2
(Г) 4
(Д) 6
Задача 18.
В прямоугольнике 1000 × 1003, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
(А) 1000
(Б) 1003
(В) 2002
(Г) 2003
(Д) 2004
Задача 19.
У Маши есть 6 карточек, на каждой из которых написано натуральное число. Она произвольно выбирает 3 карточки и вычисляет сумму чисел, написанных на них. Проделав это для всех 20 возможных комбинаций из трёх карточек, она обнаружила, что 10 сумм равны 16, а остальные 10 сумм — 18. Тогда наименьшее из чисел на карточках равно
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 20.
На чертеже изображены две параболы. Их вершины лежат на прямой, параллельной оси ОУ. Одна из них имеет уравнение $y = ax^2 + bx + c$, а уравнение второй параболы имеется среди уравнений:
(1) $y = − ax^2 − bx + c$
(2) $y = − 2ax^2 − bx + c$
(3) $y = − 2ax^2 − 2bx + c$
(4) $y = − 2ax^2 + 2bx + c$
(5) $y = − ax^2 + cx + b$
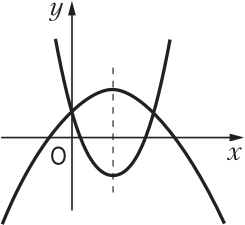
Каково уравнение второй параболы?
(А) (1)
(Б) (2)
(В) (3)
(Г) (4)
(Д) (5)
Задача 21.
На рисунке изображены 4 пересекающихся квадрата со сторонами 11, 9, 7 и 5 см. На сколько сумма площадей двух серых областей больше суммы площадей двух чёрных областей?

(А) 25 см2
(Б) 36 см2
(В) 64 см2
(Г) 0
(Д) невозможно определить
Задача 22.
На книжной полке стоят 50 книг по математике и физике. Никакие 2 книги по физике не стоят рядом, но рядом с каждой книгой по математике стоит другая книга по математике. Какое из следующих утверждений может быть неверным?
(А) книг по математике хотя бы 32
(Б) книг по физике не более 17
(В) есть 3 книги по математике, стоящие подряд
(Г) если книг по физике 17, то одна из них — первая или последняя на полке
(Д) среди любых 9 стоящих подряд книг хотя бы 6 — по математике
Задача 23.
Известно, что $a$ ≠ 0, $a$ ≠ 1, $a$ ≠ −1. Какое число из (А)-(Д) не может быть самым большим в этом наборе?
(А) $\displaystyle \frac{1}{a}$
(Б) $\sqrt[3]{a^2}$
(В) $\displaystyle \frac{1}{\sqrt[3]{a^2}}$
(Г) $a^2$
(Д) $a^3$
Задача 24.
Имеется 6 палочек с длинами 2, 4, 4, 10, 22, 37 см. Сколько различных равнобедренных трапеций можно сложить, каждый раз используя все палочки?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 25.
Маша старше Миши ровно на один месяц (дни их рождения приходятся на одно и то же число в двух соседних месяцах), а Даша старше Миши на столько же дней, на сколько Маша старше Даши. В каком месяце не могла родиться Даша?
(А) в апреле
(Б) в мае
(В) в июле
(Г) в августе
(Д) в декабре
Задача 26.
Каково наибольшее возможное значение площади выпуклого четырёхугольника, если длины его последовательных сторон равны 1, 4, 7 и 8?
(А) 12
(Б) 14
(В) 16
(Г) 18
(Д) 30
Задача 27.
Сколько различных пар вещественных чисел (х, у) удовлетворяют уравнению (х + у)2 = (х + 3) ⋅ (у – 3)?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) бесконечно много
Задача 28.
Разглядывая 6 одинаковых монет, которые лежат на столе и не касаются друг друга, Вася обнаружил, что некоторые из них «заперты»: никакую из них нельзя сдвинуть со стола, не задевая других монет. Какое наибольшее количество «запертых» монет он мог увидеть?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 29.
Сколько существует таких натуральных n, что остаток от деления 2003 на n равен 23?
(А) 22
(Б) 19
(В) 13
(Г) 12
(Д) 87
Задача 30.
На координатной плоскости нарисовали прямые у = 2, у = 2х и параболу y = х2 + bх + с. Потом координатные оси стёрли. Получился рисунок, изображённый справа. Какое из следующих соотношений возможно?
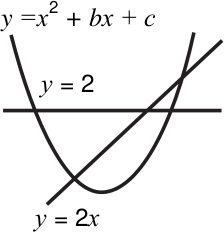
(А) с = 3
(Б) b = −2
(В) b + c > 1
(Г) b2 < 4c – 9
(Д) b + c < −2

