Задача 1.
Сначала восемь кенгуру сидели так, как показано на рисунке. Потом некоторые из них перепрыгнули на свободные квадратики так, что в каждой строке и каждом столбце оказалось ровно по два кенгуру. Какое наибольшее количество кенгуру при этом могли остаться на своих местах?

(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 2.
$\sqrt[3]{x\sqrt{x}}$ равно:
(А) $x^{\frac{2}{3}}$
(Б) $x^{\frac{1}{6}}$
(В) $x^{\frac{1}{3}}$
(Г) $x^{\frac{1}{2}}$
(Д) $x^{\frac{5}{6}}$
Задача 3.
В концерте участвовали 4 солиста, 3 дуэта, 2 трио и 1 квартет. Сколько музыкантов участвовали в концерте?
(А) 10
(Б) 16
(В) 20
(Г) 24
(Д) 30
Задача 4.
В прямоугольном треугольнике с катетами а и b на гипотенузу c опущена высота h. Какое соотношение обязательно верно?
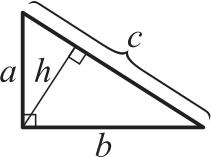
(А) ab = h2
(Б) a + b = c + h
(В) bh = ac
(Г) ch = ab
(Д) ни одно из указанных
Задача 5.
Сотрудники фирмы «Бурундук» уходят в отпуск на целый месяц, если этот месяц начинается и кончается одним и тем же днём недели. Сколько месяцев будут отдыхать сотрудники фирмы с 1 января 2005 года по 31 декабря 2015 года?
(А) 0
(Б) 1
(В) 2
(Г) 11
(Д) 132
Задача 6.
Какое из следующих чисел является кубом натурального числа?
(А) 6,4 ⋅ 1011
(Б) 6,4 ⋅ 1013
(В) 6,4 ⋅ 1014
(Г) 6,4 ⋅ 1015
(Д) 6,4 ⋅ 1018
Задача 7.
С полуночи до полудня Ученый Кот рассказывает сказки, а с полудня до полуночи – спит под дубом. На дубе том висит плакат: «Два часа назад Кот делал то же самое, что будет делать через час». В какой из указанных моментов времени надпись на плакате верна?
(А) 1:30
(Б) 23:30
(В) 0:30
(Г) 22:30
(Д) 13:30
Задача 8.
Пусть $x>1$ и $0<y<1$. Какое из следующих чисел самое маленькое?
(А) $xy$
(Б) $\displaystyle \frac{x}{y}$
(В) $\displaystyle \frac{y}{x}$
(Г) $\displaystyle \frac{x^2}{y^2}$
(Д) $\displaystyle \frac{y^2}{x^2}$
Задача 9.
Каждый из двух согнутых кусков проволоки состоит из 8 участков длины 1. Один из кусков наложили на другой так, что они частично совпали. Какова наибольшая возможная длина их общей части?
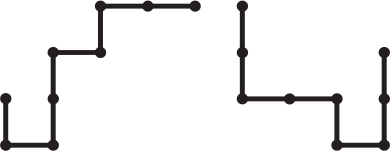
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 10.
Пусть $A = \sin^2\alpha + \sin^2\beta$, $B = \cos^2\alpha + \cos^2\beta$. Какой из вариантов возможен?
(А) $A = 1$, $\displaystyle B = \frac{3}{2}$
(Б) $\displaystyle A = \frac{3}{4}$, $\displaystyle B = \frac{5}{4}$
(В) $\displaystyle A = \frac{3}{2}$, $\displaystyle B = \frac{4}{3}$
(Г) $A = 2$, $B = 2$
(Д) никакой из перечисленных
Задача 11.
Если х – квадрат натурального числа, то следующий квадрат натурального числа – это:
(А) х + 1
(Б) х2 + 1
(В) х2 + 2х + 1
(Г) х2 + х
(Д) x + 2√x + 1
Задача 12.
Жан-Кристоф продолжает изучать русский язык. Он выписывает подряд натуральные числа словами до тех пор, пока не напишет первое число, в записи которого участвуют все буквы слова «число». Чему равна сумма цифр числа, на котором Жан-Кристоф остановится?
(А) 5
(Б) 8
(В) 9
(Г) 11
(Д) 30
Задача 13.
На рисунке изображены три полуокружности радиуса 2. Точки А и B расположены в точности над центрами E и F двух нижних полуокружностей. Чему равна площадь закрашенной области?
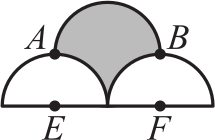
(А) 2π
(Б) 7
(В) 2π + 1
(Г) 8
(Д) 2π + 2
Задача 14.
Числа a и b таковы, что 4 ≤ a ≤ 6, 1 ≤ b ≤ 2 . Какое из следующих чисел обязательно меньше 9?
(А) 2a − 3b
(Б) a + 2b
(В) 3a − b
(Г) 8b − 2a
(Д) 13b − a
Задача 15.
Игральный кубик, сумма очков на противоположных гранях которого равна 7, прокатили по клетчатой дорожке. Начальное положение кубика и дорожка изображены на рисунке. Сколько очков оказалось на верхней грани кубика в конце пути?
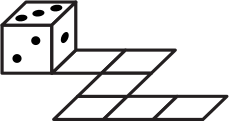
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 16.
Если многоугольник (возможно, невыпуклый) составлен из 8 одинаковых правильных треугольников, то он не может быть
(А) семиугольником
(Б) шестиугольником
(В) трапецией
(Г) ромбом
(Д) треугольником
Задача 17.
Пусть p – наименьшее простое число, которое равно сумме трёх различных простых чисел: p = p1 + p2 + p3. Тогда произведение p1 ⋅ p2 ⋅ p3 равно:
(А) 30
(Б) 165
(В) 105
(Г) 231
(Д) 385
Задача 18.
Трапеция АВСD с основанием АВ вписана в окружность. Угол АDВ равен 65º, а угол DВС равен 35º. Тогда угол А равен:
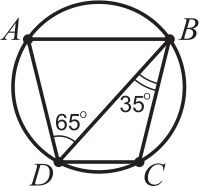
(А) 70º
(Б) 75º
(В) 80º
(Г) 105º
(Д) невозможно определить
Задача 19.
Имеется набор гирь, в котором самая тяжёлая гиря в 5 раз тяжелее среднего веса всех гирь. Чему не может равняться количество гирь в наборе?
(А) 15
(Б) 11
(В) 8
(Г) 6
(Д) 4
Задача 20.
Каждая пара вершин куба соединена отрезком. Сколько различных середин у всех этих отрезков?
(А) 8
(Б) 12
(В) 18
(Г) 19
(Д) 28
Задача 21.
Пусть $S$ – площадь поверхности Земли, а $S_0$ – площадь той её части, точки которой ближе к Петербургу, чем к центру Земли. Тогда
(А) $\displaystyle \frac{S_0}{S}>\frac{1}{2}$
(Б) $\displaystyle \frac{S_0}{S} = \frac{1}{2}$
(В) $\displaystyle \frac{1}{3}<\frac{S_0}{S}<\frac{1}{2}$
(Г) $\displaystyle \frac{S_0}{S} = \frac{1}{3}$
(Д) $\displaystyle \frac{S_0}{S}<\frac{1}{3}$
Задача 22.
Сколько существует треугольников, у которых одна из сторон равна 3 см, другая — 4 см, а один из углов равен 10º?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 23.
На чертеже ниже показана зависимость у − x от у + x.
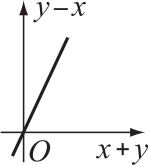
На каком из графиков А-Д изображена зависимость у от x?
(А) 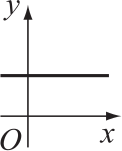
(Б) 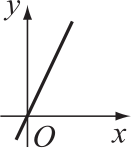
(В) 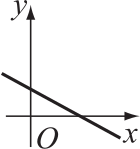
(Г) 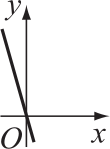
(Д) 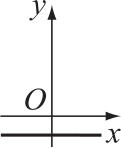
Задача 24.
Гусеница выползла из домика в полдень и ползёт по лугу, поворачивая через каждый час на 90º направо или налево. За первый час она проползла 1 м, за второй — 2 м, и т.д. На каком наименьшем расстоянии от домика она могла оказаться в 10 часов вечера?
(А) 0 м
(Б) 1 м
(В) 2 м
(Г) √5 м
(Д) √61 м
Задача 25.
По определению, n! = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n. Какой сомножитель нужно вычеркнуть из произведения 1! ⋅ 2! ⋅ 3! ⋅ 4! ⋅ …⋅ 100!, чтобы оставшееся произведение стало квадратом некоторого натурального числа?
(А) 13!
(Б) 42!
(В) 47!
(Г) 50!
(Д) это невозможно
Задача 26.
Каждая парабола у = ax2 + bx + c разбивает плоскость на две части. Если две точки попадают в разные части, то будем говорить, что парабола разделяет эти точки. Какие две точки не могут быть разделены никакой параболой вида у = ax2 + x, a > 0?
(А) (−1; 1) и (1; −1)
(Б) (−1; 0) и (1; 0)
(В) (−8; 0) и (−1; 0)
(Г) (3; 0) и (5; 0)
(Д) все пары А-Г могут быть разделены
Задача 27.
На белой клетчатой доске 10 × 10 Вася закрасил 10 клеток синим цветом, а несколько других клеток – красным цветом. Оказалось, что никакие две клетки красного и синего цвета не имеют общей стороны. Какое наименьшее число клеток могли остаться незакрашенными?
(А) 10
(Б) 7
(В) 6
(Г) 5
(Д) 3
Задача 28.
Про набор чисел $a + 2$, $\displaystyle − \frac{2}{a}$, 6, $a^2$ известно, что два из этих чисел равны, а ещё одно ровно вдвое больше их. Тогда
(А) $\displaystyle a + 2 = − \frac{2}{a}$
(Б) $\displaystyle – \frac{2}{a} = 6$
(В) $\displaystyle – \frac{2}{a} = a^2$
(Г) $a^2 = a + 2$
(Д) это невозможно
Задача 29.
На картинке изображены графики функций $f(x)$, $g(x)$ и ещё одной. Какой?
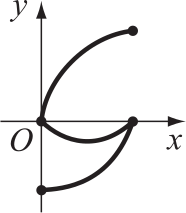
(А) $f(x) + g(x)$
(Б) $f(x) − g(x)$
(В) $f(x)⋅g(x)$
(Г) $\displaystyle \frac{f(x)}{g(x)}$
(Д) $ − f(x)⋅g(x)$
Задача 30.
Найдите тупой угол треугольника, в котором центры вписанной и описанной окружностей симметричны относительно некоторой стороны этого треугольника.
(А) 100º
(Б) 108º
(В) 120º
(Г) 136º
(Д) 150º

