Задача 1.
Клара посчитала сумму цифр, с помощью которых записывается сегодняшняя дата: 28.10.2018. Сколько в этом году дат с такой же суммой цифр?
Задача 2.
На рынке продавались арбузы, общим весом 100 кг. Суммарный вес трёх самых лёгких арбузов — 25 кг, а трёх самых тяжёлых — 35 кг. Каждый арбуз может весить нецелое число килограмм. Сколько арбузов могло продаваться на рынке?
Задача 3.
Лена и Оля научились рисовать параллельные отрезки внутри квадрата. Сначала Лена провела два отрезка на равном расстоянии от сторон исходного квадрата, а потом Оля провела два отрезка на равном расстоянии от сторон образовавшегося в центре прямоугольника. В результате образовался серый прямоугольник с соотношением сторон 2 : 1. Известно, что меньшая сторона серого прямоугольника равна 24 см и она в 3 раза меньше выделенного отрезка. Найдите длину неизвестного отрезка.
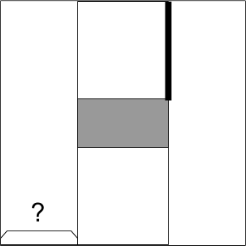
Задача 4.
Ниф-Ниф, Наф-Наф и Нуф-Нуф собирали грибы — мухоморы и поганки. Ниф-Ниф собрал 26 мухоморов, а Нуф-Нуф — 17 поганок. Известно, что всего мухоморов было собрано столько, сколько нашли грибов вместе Наф-Наф и Нуф-Нуф. Сколько поганок собрал Наф-Наф?
Задача 5.
У учительницы есть 50 карточек с числами от 1 до 50. Она раздает по две карточки 25 ученикам. При этом ученик становится счастливым, если числа на его карточках отличаются более чем в два раза. Может ли учительница сделать всех учеников счастливыми?
Задача 6.
В одной комнате собралось больше 20 человек, каждый рыцарь или лжец. Все люди произнесли фразу: «Среди всех остальных, не считая меня, не больше пяти рыцарей и не меньше десяти лжецов». Сколько рыцарей могло находиться в комнате? (Рыцари всегда говорят только правду, лжецы всегда врут.)
Задача 7.
Кирилл написал на доске всевозможные 9-значные числа, в записи которых встречаются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 по одному разу. Мефодий выбрал из них самое большое и самое маленькое и стёр их. Потом он выбрал самое большое и самое маленькое из оставшихся чисел и тоже их стёр. Мефодий повторял свои действия до тех пор, пока на доске не осталось два числа. Какие это числа?
Задача 8.
В клетках «лестницы» расставлены числа 1, 1, 2, 2, 2, 3, 4, 4, 5, 6, так что сумма чисел в каждом столбце, кроме самого левого, на 1 больше, чем в предыдущем. Сколько существует различных расстановок?

