Задача 1.
Напишите наибольшее число с разными цифрами, у которого соседние цифры отличаются не менее, чем на 2.
Задача 2.
Обезьянкам Анфисе, Дусе и Мусе дали бананы − всего в сумме не более 10. Анфиса дала 1 банан Дусе и 2 банана Мусе, после чего у всех стало поровну. Какое количество бананов могло быть у Анфисы изначально? (Укажите все варианты)
Задача 3.
Закрасьте две клетки, чтобы получить верное математическое равенство. Закрашенная клетка не участвует в вычислениях и может быть в любом месте, даже между цифрами числа (« / » − знак деления).

Задача 4.
Лёша и Костя ели пиццу – им привезли 4 штуки: диаметра 28 см, 18 см, 16 см и 6 см – подарок за заказ. Лёша съел самую большую и самую маленькую, а Костя – две средних. Кто съел больше?
Задача 5.
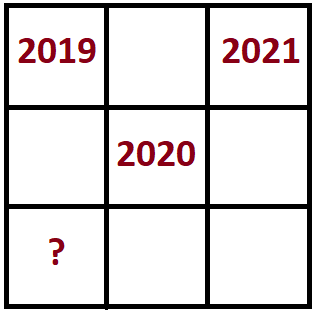
В Новом Году Дед Мороз хочет составить магический квадрат, в котором суммы чисел в столбцах, строках и двух больших диагоналях одинаковы. Заполните квадрат до конца.
Задача 6.
В городе Полоссити на всех дорогах странная разметка: первая полоска длиной 1 м, затем разрыв 1 м, затем полоска длиной 2 м, снова разрыв 1 м, затем полоска 3 м, разрыв, … и так далее, пока дорога не кончится. Если в конце не хватает длины дороги, то полоска просто обрывается.

Разметку сделали вдоль набережной протяженностью 2020 метров.
- Сколько полосок в разметке вдоль набережной?
- Какова длина последней полоски?
Задача 7.
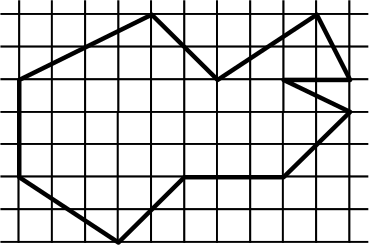
Отметьте на линиях сетки две точки, чтобы они разделили данную ломаную на два куска одинаковой длины.
Задача 8.
Чтобы войти в подземелье, Гарри Поттер сделал из одинаковых магических кубиков амулет, как на рисунке. Но коварный Драко Малфой проделал своей волшебной палочкой шесть сквозных отверстий, каждое из которых прошло ровно через шесть кубиков (параллельно рёбрам маленьких кубиков).
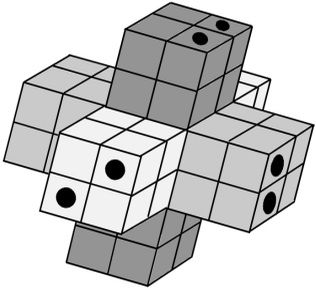
- Сколько маленьких магических кубиков осталось неповреждёнными, если внутри амулета нет пустот?
- Сколько маленьких кубиков проткнули три раза?
Задача 9.
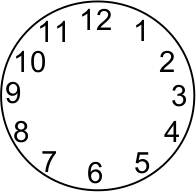
На радужной фабрике для сборки настенных часов (см. рисунок) нужен комплект из 15 пластмассовых цифр 15 разных цветов. Сколько различных циферблатов можно изготовить на этой фабрике, если все комплекты абсолютно одинаковы?
Задача 10.
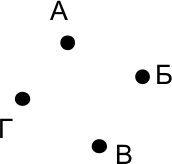
В компании из четырёх человек:
- Алёша заявил: «У меня тут нет друзей».
- Боря подхватил: «А у меня тут ровно 1 друг».
- Вася добавил: «А у меня ровно 2 друга».
- Гоша сказал: «А у меня 3 друга!»
Оказалось, что все, у кого чётное количество друзей, сказали правду, а те, у кого нечётное − соврали. Нарисуйте, кто с кем дружит.