Задача 1.
В слове МАТЕМАТИКА стёрли 6 букв (возможно, среди них были одинаковые). Оставшиеся буквы переписали в обратном порядке. Что не могло получиться?
(А) КАМА
(Б) КИМА
(В) АТЕМ
(Г) ТЕМА
(Д) ТАЕТ
Задача 2.
В клетках квадрата 4 × 4 написали цифры 0 и 1 так, что в каждой строке и каждом столбце оказалось по 2 единицы и по 2 нуля. Потом некоторые цифры стёрли, а две — обозначили буквами Х и У. Чему равны Х и У?
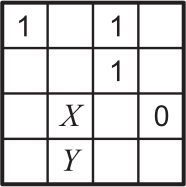
(А) Х = У = 1
(Б) Х = 1, У = 0
(В) Х = 0, У = 1
(Г) Х = У = 0
(Д) невозможно определить
Задача 3.
Чем является число 27 для числа 3?
(А) квадратом
(Б) треугольником
(В) кругом
(Г) кубом
(Д) шаром
Задача 4.
В треугольнике АВС точка D — середина АВ, E — середина DВ, F — середина ВС. Если площадь треугольника АВС равна 96, то площадь треугольника АEF равна
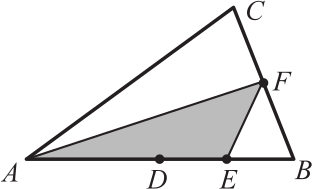
(А) 16
(Б) 24
(В) 32
(Г) 36
(Д) 48
Задача 5.
При возведении в квадрат
(А) число всегда увеличивается
(Б) число всегда уменьшается
(В) число всегда изменяется
(Г) изменяются все числа, кроме одного
(Д) изменяются все числа, кроме двух
Задача 6.
Пусть $x$∗$y$ = $x\sqrt{y}$. Чему равно ($\sqrt{18}$∗2)∗3 ?
(А) 6$\sqrt{2}$
(Б) 6
(В) 6$\sqrt{3}$
(Г) 18$\sqrt{2}$
(Д) 18
Задача 7.
Народная примета племени Уа-Уа гласит: «Если крокодилы едят быстро, то скоро будет дождь». Это означает, что
(А) если дождя не ожидается, а крокодилы едят, то они едят не быстро
(Б) если в местности нет крокодилов, то там не бывает дождя
(В) если собирается дождь, то крокодилы едят быстро
(Г) если крокодилы едят медленно, то дождя не будет
(Д) если крокодилы воздерживаются от еды, то дождя не будет
Задача 8.
Число 10100 назовём гигантом. Чему равно число 1000100 ?
(А) 100 гигантов
(Б) 3 гиганта
(В) гигант3
(Г) гигант2
(Д) гигантгигант
Задача 9.
ABCD — квадрат, а CDF — правильный треугольник. Чему равен угол BAF?
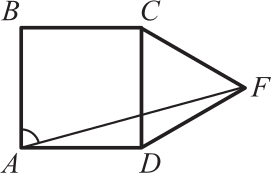
(А) 60°
(Б) 75°
(В) 85°
(Г) 67°30'
(Д) другой ответ
Задача 10.
Натуральные числа, большие 2007, возвели в квадрат и у каждого квадрата вычислили сумму цифр. Самая маленькая из этих сумм равна
(А) 27
(Б) 19
(В) 2007
(Г) 1
(Д) другой ответ
Задача 11.
Чему равно число 9999994 ⋅ 9999995 − 9999990 ⋅ 9999999?
(А) 0
(Б) 20
(В) 180
(Г) 990
(Д) 9999990
Задача 12.
Прямоугольный треугольник таков, что длина его гипотенузы равна сумме квадратов длин его катетов. Чему равен радиус окружности, описанной около этого треугольника?
(А) 1
(Б) 1/2
(В) 1/3
(Г) такого треугольника не существует
(Д) невозможно определить
Задача 13.
Каждая из трёх окружностей на чертеже касается двух других. Радиус большей окружности равен 6. Какова сумма расстояний между центрами?
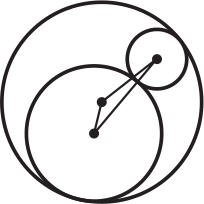
(А) 12
(Б) 9
(В) 6
(Г) 3
(Д) невозможно определить
Задача 14.
Пусть N — наименьшее из натуральных чисел, обладающих следующим свойством: 10N является квадратом некоторого натурального числа, а 6N — кубом. Чему равна сумма первой и последней цифр числа N?
(А) 3
(Б) 5
(В) 6
(Г) 8
(Д) 13
Задача 15.
Пусть число $m$ – один из корней уравнения $x^3 + 1 = 2007x$. Какое из чисел наверняка является корнем уравнения $x^3 + 1 = 2007x^2$ ?
(А) $\displaystyle \frac{8}{5}m$
(Б) $\displaystyle \frac{5}{2}m$
(В) $m^2$
(Г) $\displaystyle \frac{1}{m}$
(Д) $m$ + 1
Задача 16.
Вася учится стрелять в тире. Месяц назад, на первом занятии, он попал 40 раз из 100. Сегодня, после месяца тренировок, он сделал 200 выстрелов и обнаружил, что его меткость (то есть доля удачных выстрелов) повысилась на 80%. Сколько раз он попал сегодня?
(А) 120
(Б) 140
(В) 144
(Г) 160
(Д) 240
Задача 17.
Маша сложила три числа: количество вершин, количество рёбер и количество граней некоторой пирамиды. Какой результат она могла получить?
(А) 28
(Б) 29
(В) 30
(Г) 31
(Д) 32
Задача 18.
Числа a и b таковы, что a > $\displaystyle \frac{1}{b}$ и $\displaystyle \frac{1}{a}$ > b. Тогда
(А) ab > 1
(Б) a < 0
(В) b > a
(Г) b < 0
(Д) такого не бывает
Задача 19.
Для некоторых трёхзначных чисел квадрат суммы цифр равен сумме квадратов этих цифр. Сколько таких чисел?
(А) 0
(Б) 9
(В) 10
(Г) 1
(Д) 90
Задача 20.
Пусть f(x) — это меньшее из чисел 2х и 6 − х. Какое самое большое значение принимает величина f(x) ?
(А) 2
(Б) 4
(В) 6
(Г) 8
(Д) наибольшего значения нет
Задача 21.
а, b, c — стороны треугольника. Известно, что (a + b + c) ⋅ (a + b − c) = 3ab. Какой угол лежит против стороны c?
(А) 150°
(Б) 30°
(В) 45°
(Г) 60°
(Д) 90°
Задача 22.
В шкатулке у Кощея Бессмертного лежит несколько одинаковых ожерелий (более одного). Он знает, что общее число бусинок на ожерельях в шкатулке меньше 300 и больше 200. Если бы Кощей знал это число точно, то, подумав, он мог бы назвать точное количество ожерелий, не открывая шкатулки. Сколько ожерелий в шкатулке?
(А) 16
(Б) 17
(В) 19
(Г) 25
(Д) невозможно определить
Задача 23.
Какое наибольшее количество вершин может быть у выпуклого многоугольника, если эти вершины лежат на поверхности куба, но сам многоугольник не лежит ни на какой грани куба?
(А) 4
(Б) 6
(В) 8
(Г) 12
(Д) 18
Задача 24.
Дом имеет размеры 4 м × 6 м. Собака, привязанная к углу дома 10-метровой верёвкой, бегает по двору. Какова площадь участка, доступного собаке?
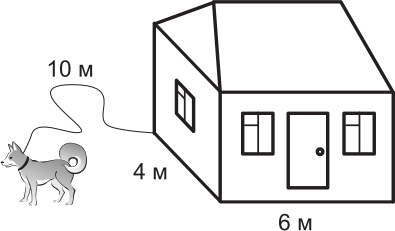
(А) 100π
(Б) 100π − 24
(В) 76π
(Г) 88π
(Д) другой ответ
Задача 25.
Сколько отрицательных чисел среди членов последовательности cos1°, cos10°, cos100°, cos1000°, ... ?
(А) 1
(Б) 2
(В) 10
(Г) 100
(Д) бесконечно много
Задача 26.
Назовем натуральное число N особым, если можно подобрать такое натуральное число M, что в записи произведения M ⋅ N все цифры одинаковы. Какое из следующих чисел не особое?
(А) 13
(Б) 14
(В) 15
(Г) 16
(Д) 18
Задача 27.
Пусть $f$ – такая функция, что уравнение $f(x) = x$ имеет ровно один корень. Какое из следующих уравнений может иметь более двух корней?
(А) $\displaystyle \frac{1}{3}f(3x) = x$
(Б) $f(f(x) + 1) = f(x) + 1$
(В) $f\left(x^2\right) = x^2$
(Г) $\sqrt[3]{f\left(x^3 − 1\right) + 1} = x$
(Д) никакое
Задача 28.
За один шаг автомат умеет выполнять одну из четырёх операций: либо умножить данное число на 2, либо умножить данное число на 3, либо возвести его в квадрат, либо в куб. Что может получиться после 5 шагов, если начать с числа 15?
(А) 28 ⋅ 35 ⋅ 56
(Б) 2 ⋅ 34 ⋅ 52
(В) 28 ⋅ 34 ⋅ 52
(Г) 2 ⋅ 32 ⋅ 56
(Д) 26 ⋅ 36 ⋅ 54
Задача 29.
Имеются одинаковые плитки кафеля с нарисованными на них дугами. Длина каждой дуги равна 1, а концы дуг — середины сторон плитки. Из 16 таких плиток надо сложить квадрат. Некоторые из дуг будут соединяться между собой, образуя более длинные кривые. Какова наибольшая возможная длина такой кривой?
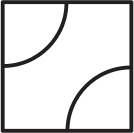
(А) 18
(Б) 20
(В) 21
(Г) 22
(Д) 24
Задача 30.
В равнобедренном треугольнике АВС с основанием АВ = 1 биссектриса, высота и медиана, проведённые из вершины А, имеют длины b, h и m соответственно. Какое из следующих равенств возможно?
(А) m = 0,7
(Б) b = 1,5
(В) h = 1,1
(Г) b = 0,6
(Д) все варианты А-Г невозможны

