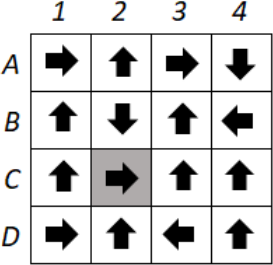
В квадрате 4 × 4 в отмеченной серым фоном клетке стоит фишка. За одно действие фишка перемещается в соседнюю по стороне клетку, по направлению стрелочки, на которой стоит. Также после каждого перемещения стрелочка в клетке, где только что была фишка, меняется на противоположную. С какой клетки фишка выйдет за границу квадрата? В ответе укажите строку и столбец этой клетки.

В соревновании по бегу участвовали пять спортсменов: 𝐴, 𝐵, 𝐶, 𝐷 и 𝐸. Было сделано два прогноза, в каком порядке они финишируют.

• Первый прогноз: 𝐴 — первый, 𝐵 — второй, 𝐶 — третий, 𝐷 — четвёртый, 𝐸 — пятый.
• Второй прогноз: 𝐶 — первый, 𝐸 — второй, 𝐴 — третий, 𝐵 — четвёртый, 𝐷 — пятый.

Оказалось, что первом прогнозе было верно предсказано ровно про троих спортсменов, а во втором — ровно про двоих. Кто какое место занял в забеге?

Три купца: Фома, Ерёма и Юлий встретились в Новгороде. Если Фома отдаст Ерёме 70 золотых монет, то у Ерёмы и Юлия будет поровну денег. Если Фома отдаст Ерёме 40 золотых монет, то у Фомы и Юлия будет поровну денег. Сколько золотых монет должен отдать Фома Ерёме, чтобы у них двоих стало поровну денег?

В прибрежной деревне 7 человек рыбачат каждый день, 8 человек рыбачат через день, 3 человека рыбачат раз в три дня, а остальные не рыбачат вовсе. Вчера рыбачили 12 человек, сегодня рыбачат 10 человек. Сколько людей будет рыбачить завтра?

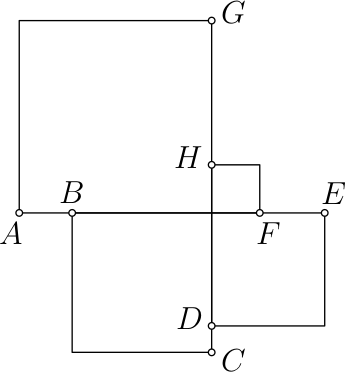
На рисунке изображено 4 квадрата. Известно, что длина отрезка 𝐴𝐵 равна 11, длина отрезка 𝐹𝐸 равна 13, длина отрезка 𝐶𝐷 равна 5. Чему равна длина отрезка 𝐺𝐻?

На фотографирование класса пришли 4 девочек и 8 мальчиков. Дети по двое подходят к фотографу и делают совместное фото. Среди какого наименьшего количества фотографий обязательно есть либо фотография двух мальчиков, либо фотография двух девочек, либо две фотографии с одними и теми же детьми?

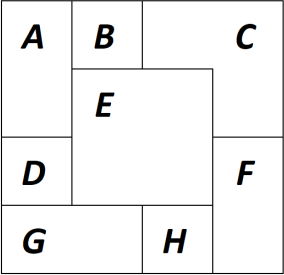
Восемь бумажных квадратов 2 × 2 последовательно выкладывали на стол, пока не получился большой квадрат 4 × 4. Последним на стол положили квадрат 𝐸. На рисунке изображено, как видны квадраты: квадрат 𝐸 видно полностью, остальные квадраты видно частично. Какой квадрат положили на стол третьим по счёту?

Натуральное число 𝑛 назовём хорошим, если 2020 при делении на 𝑛 даёт остаток 22. Сколько существует хороших чисел?