Задача 1.
Какой из квадратов поделён на две неравные по площади фигуры?
(А) 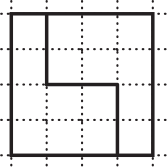
(Б) 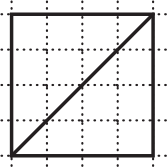
(В) 
(Г) 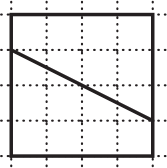
(Д) 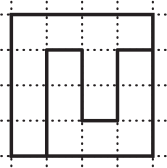
Задача 2.
Пожарному необходимо добраться до огня. Передвигаться он может только двумя способами: по горизонтальным поверхностям и по лестницам (перепрыгивать, подпрыгивать или как-то иначе перемещаться нельзя). Какое наименьшее количество лестниц он должен преодолеть?
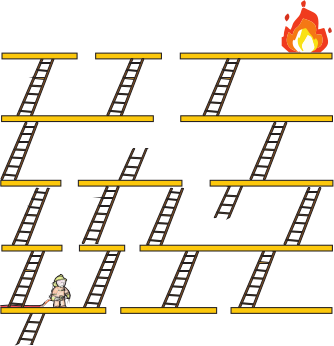
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 3.
Таблица состоит из 28 белых клеток. Ира закрасила 2 горизонтальных ряда и 1 вертикальный. Сколько клеток осталось не закрашено?

(А) 8
(Б) 10
(В) 12
(Г) 14
(Д) 17
Задача 4.
Футболисты с номерами от 1 до 11 встали в круг по порядку. Каждый игрок, получивший мяч, передаёт его третьему игроку слева от себя. Начинает футболист с номером 1. Игра продолжается до тех пор, пока какой-либо игрок не получит мяч во второй раз. Футболист с каким номером ударит по мячу последним?
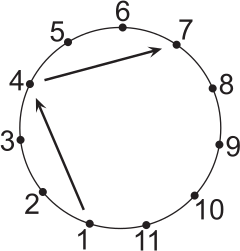
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 5.
Миша написал три последовательных четырёхзначных числа. Но его сестра стёрла некоторые цифры. Какие цифры (по порядку слева направо) она стёрла?

(А) 389, 3, 99
(Б) 489, 3, 96
(В) 489, 4, 98
(Г) 489, 4, 99
(Д) 488, 4, 99
Задача 6.
Лиза заплатила за три наклейки для альбома 7 рублей. Цена каждой наклейки – целое число, и все три цены различны. Сколько стоила самая дорогая наклейка?
(А) 2 рубля
(Б) 3 рубля
(В) 4 рубля
(Г) 5 рублей
(Д) 6 рублей
Задача 7.
Кошка сбросила с конструкции один кубик. Как выглядела конструкция до того, как кубик был сброшен?
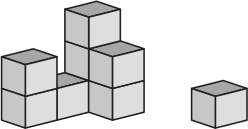
(А) 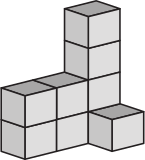
(Б) 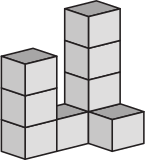
(В) 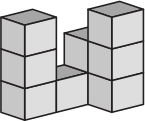
(Г) 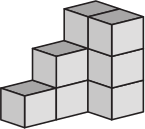
(Д) 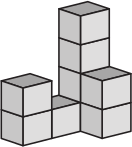
Задача 8.
На стене, выложенной белыми и серыми квадратными плитками, висит плакат конкурса «Кенгуру». Сколько серых плиток закрыто плакатом?
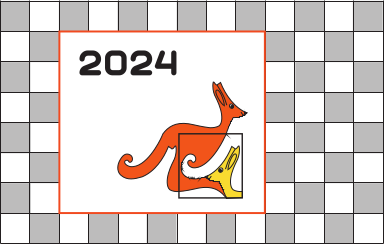
(А) 15
(Б) 21
(В) 25
(Г) 36
(Д) 42
Задача 9.
Тоня и Дима играют, подбрасывая монетку и шагая по клеткам, начиная с номера 1. Если у монеты выпадает сторона X, то игроку нужно сделать три шага вперёд по клеткам. Если выпадет сторона Y, игрок должен сделать шаг назад или остаться на старте.
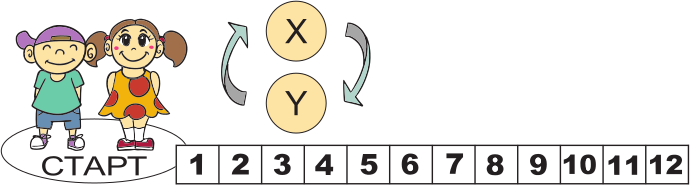
Каждый из игроков подбросил монетку четыре раза. В результате Тоня оказалась на клетке с номером 4, а Дима на клетке с номером 8. Сколько раз у обоих игроков суммарно выпала сторона монетки Y?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 10.
На тарелке лежит пять разных фруктов и ягод:  . Аня любит
. Аня любит  . Боря любит
. Боря любит  . Коля любит
. Коля любит  . Денис любит
. Денис любит  . Эльза любит
. Эльза любит  .
.
Каждый из ребят взял с тарелки что-то одно из того, что он любит. При этом все они взяли разные фрукты или ягоды. Что взял Боря?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 11.
Алла построила башню из 8 дисков.
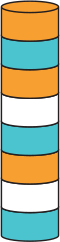
Затем она стала последовательно убирать диски: сначала второй диск снизу, затем третий диск снизу новой башни, затем четвёртый диск снизу получившейся башни, затем пятый диск снизу оставшейся башни. Какая башня получилась у Аллы в итоге?
(А) 
(Б) 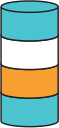
(В) 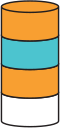
(Г) 
(Д) 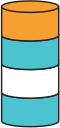
Задача 12.
Пингвин каждый день ходит на рыбалку и приносит 9 рыб для своих двух птенцов. Каждый день он даёт первому увиденному птенцу 5 рыб, а второму – 4 рыбы. Пингвинята съедают сразу всех рыб. За последние несколько дней один птенец съел 26 рыб. Сколько рыб съел за эти дни другой птенец?
(А) 19
(Б) 22
(В) 25
(Г) 28
(Д) 31
Задача 13.
В четырёх кругах разложено семь карт. На картах написаны числа от 1 до 7 по одному числу на каждой карте. Сумма чисел в каждом круге равна 10. Какое число написано на карте со знаком вопроса?
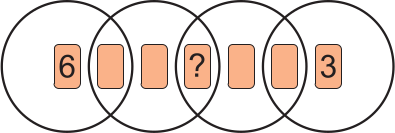
(А) 1
(Б) 2
(В) 4
(Г) 5
(Д) 7
Задача 14.
Из пяти деталей пазла Лина хочет составить гусеницу, у которой будут голова, хвост и между ними туловище, состоящее из одной, двух или трёх деталей. Сколько различных гусениц может составить Лина так, чтобы детали пазла точно подходили друг другу?

(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 15.
Фокусник написал числа от 1 до 4 на листке бумаги. Затем он перевернул листок и на обратной стороне написал числа от 5 до 8. После этого он разрезал листок бумаги на четыре прямоугольные карты и положил их на стол. Чему равна сумма чисел, закрытых знаками вопроса?
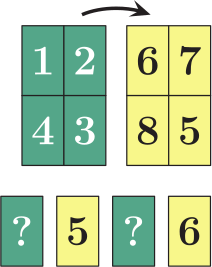
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 16.
Пол выложен плитками двух видов:  и
и  . Размеры прямоугольной плитки 23 см х 11 см. На рисунке вы можете видеть часть этого пола. Чему равна длина стороны квадратной плитки?
. Размеры прямоугольной плитки 23 см х 11 см. На рисунке вы можете видеть часть этого пола. Чему равна длина стороны квадратной плитки?
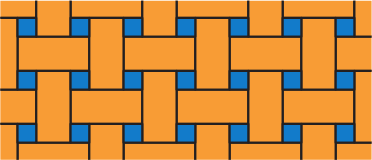
(А) 3 см
(Б) 4 см
(В) 5 см
(Г) 6 см
(Д) 7 см
Задача 17.
У Саши есть три карточки с трёхзначными числами. Сумма этих трёх чисел равна 782. Позже на каждой карточке вырезали по одной цифре. Чему равна сумма вырезанных цифр?

(А) 8
(Б) 9
(В) 10
(Г) 11
(Д) 12
Задача 18.
Люся взвешивает несколько фигур. Сколько весят все три фигуры вместе?

(А) 270 г
(Б) 280 г
(В) 290 г
(Г) 300 г
(Д) 310 г
Задача 19.
В поездке участвует 60 учеников. На каждом надета жёлтая или зелёная футболка и у каждого есть красный, синий или оранжевый рюкзак. Когда ученики выстраиваются в ряд, цвета их футболок чередуются: жёлтая, зелёная, жёлтая, зелёная и так далее. Цвета их рюкзаков при этом тоже чередуются: красный, синий, оранжевый, красный, синий, оранжевый и так далее. У скольких учеников в жёлтой футболке есть оранжевый рюкзак?
(А) 3
(Б) 4
(В) 6
(Г) 8
(Д) 10
Задача 20.
В следующих равенствах одинаковые фигуры обозначают одинаковые цифры, а разные фигуры обозначают разные цифры. Чему будет равно произведение?
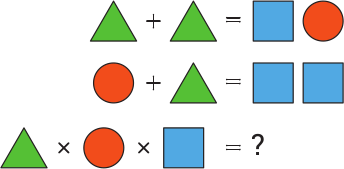
(А) 0
(Б) 12
(В) 18
(Г) 28
(Д) 30
Задача 21.
В каждой строке и каждом столбце квадрата сидит по две лягушки. Они договорились между собой, что две из них одновременно перепрыгнут на пустые соседние клетки так, чтобы после этого по-прежнему в каждой строке и каждом столбце оставалось бы ровно по две лягушки. Клетки считаются соседними, если они имеют общую сторону. Сколькими способами лягушки могут это сделать?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 22.
На рисунке изображены соты, состоящие из 9 ячеек. В некоторых из этих ячеек есть мёд. Число на каждой ячейке обозначает, в скольких соседних ячейках находится мёд. Ячейки считаются соседними, если у них есть хотя бы одна общая сторона. Сколько всего ячеек содержат мёд?
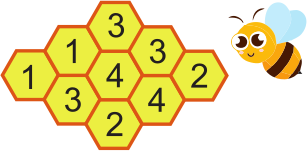
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 23.
Три девочки по очереди берут печенье с подноса, изображённого на рисунке.

Юля берёт все сердечки, которые есть на подносе. Света – все белые печенья. Алина – все большие печенья. Порядок, в котором девочки подходили к подносу, не известен. Но известно, что одна из них взяла 3 печенья, другая – 6 печений, а третья – 7 печений. Какой набор печений взяла одна из девочек?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 24.
Имеются детали двух видов: белые 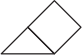 и красные
и красные  . Из четырёх белых деталей можно составить кубик. Из одной красной и одной белой деталей также можно составить кубик. Большой куб на картинке составлен из таких кубиков. Какое наименьшее количество белых деталей нужно, чтобы составить этот большой куб?
. Из четырёх белых деталей можно составить кубик. Из одной красной и одной белой деталей также можно составить кубик. Большой куб на картинке составлен из таких кубиков. Какое наименьшее количество белых деталей нужно, чтобы составить этот большой куб?
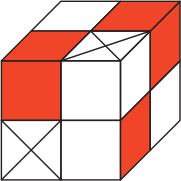
(А) 8
(Б) 11
(В) 13
(Г) 14
(Д) 23

