Задача 1.
Валера заполняет таблицу числами от 1 до 40 подряд, как показано на рисунке. Какой кусочек он сможет вырезать из таблицы, когда заполнит её до конца?
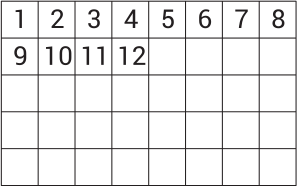
(А) 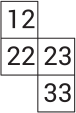
(Б) 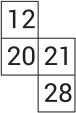
(В) 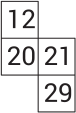
(Г) 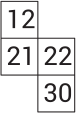
(Д) 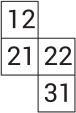
Задача 2.
Кенгуру составляет числа из спичек. Цифры от 0 до 9 он всегда составляет так, как показано на рисунке. Например, чтобы составить таким способом число 15 или 8, ему потребуется семь спичек. Какое наибольшее положительное число кенгуру может составить из семи спичек?

(А) 31
(Б) 51
(В) 74
(Г) 711
(Д) 800
Задача 3.
У Иры есть развёртка, из которой она складывает кубик. Какой из следующих пяти кубиков у неё получился из этой развёртки?
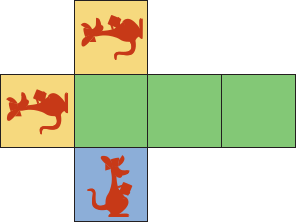
(А) 
(Б) 
(В) 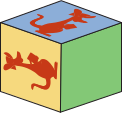
(Г) 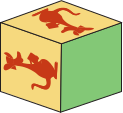
(Д) 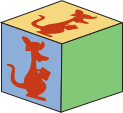
Задача 4.
Альпинист взбирается по цилиндрической башне снизу вверх. Его путь отмечен на рисунке чёрным цветом. Все шаги альпиниста одинакового размера. Девять шагов видны на изображении. Сколько его шагов не видны?

(А) 9
(Б) 10
(В) 11
(Г) 12
(Д) 13
Задача 5.
У Саши есть пять дисков разных размеров. Он хочет построить такую башню из четырёх дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Саша может построить?
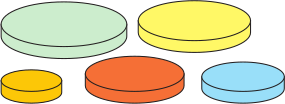
(А) 4
(Б) 5
(В) 9
(Г) 12
(Д) 20
Задача 6.
На рисунке изображена посылка, вокруг которой обвязаны четыре ленты, отмеченные буквами M, N, P и Q. В каком порядке от первой к последней завязывали эти ленты?
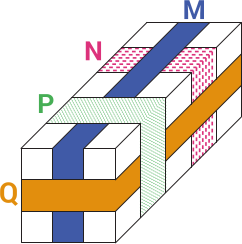
(А) M, N, Q, P
(Б) N, M, P, Q
(В) N, Q, M, P
(Г) N, M, Q, P
(Д) Q, N, M, P
Задача 7.
У Алисы есть 4 кусочка пазла. Какие два кусочка она должна сложить вместе, чтобы получить шестиугольник?
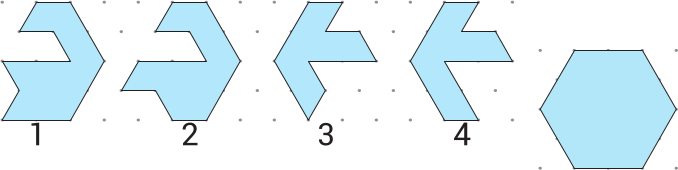
(А) 1 и 2
(Б) 1 и 3
(В) 2 и 3
(Г) 2 и 4
(Д) 1 и 4
Задача 8.
Диск с трёмя отверстиями накладывают на циферблат часов и вращают вокруг центра. Какие ещё три числа можно увидеть одновременно?
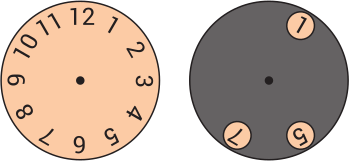
(А) 2, 4 и 9
(Б) 1, 5 и 10
(В) 4, 6 и 12
(Г) 3, 6 и 9
(Д) 5, 7 и 12
Задача 9.
Вова наклеил три кусочка бумаги 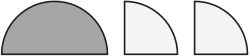 поверх круга
поверх круга  . Какую из изображённых фигур он не мог получить?
. Какую из изображённых фигур он не мог получить?
(А) 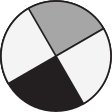
(Б) 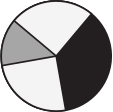
(В) 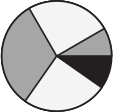
(Г) 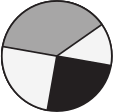
(Д) 
Задача 10.
На улице находится 7 домов, в которых живут 25 человек. В каждом доме живёт или 3, или 4 человека. В скольких домах живёт по 3 человека?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 11.
Зоя записала три последовательных двузначных числа в порядке возрастания, но вместо цифр использовала символы. У неё получилось:  ,
,  ,
,  . Какое число она запишет следующим?
. Какое число она запишет следующим?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 12.
Площадка выложена квадратными плитками трёх разных размеров. Самый маленький квадрат имеет периметр 80 мм. Уж решил отдохнуть на площадке, расположившись так, как показано на рисунке. Какова длина ужа?
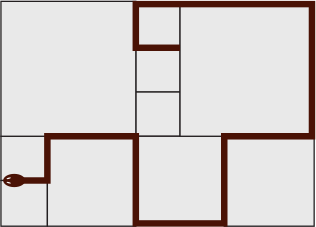
(А) 380 мм
(Б) 400 мм
(В) 420 мм
(Г) 440 мм
(Д) 460 мм
Задача 13.
Посмотрев в зеркало, Аня увидела отражение часов, которые находятся у неё за спиной: 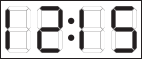 . Какое время будет в отражении, когда Аня посмотрит в зеркало через 30 минут?
. Какое время будет в отражении, когда Аня посмотрит в зеркало через 30 минут?
(А) 
(Б) 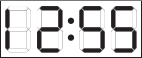
(В) 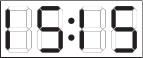
(Г) 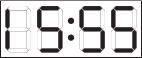
(Д) 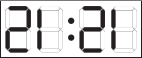
Задача 14.
Маша, Петя, Рома и Таня играли в футбол, и один из них разбил окно. Когда их спросили, кто это сделал, получили следующие ответы:
- Маша: «Это был Петя»;
- Петя: «Это был Рома»:
- Рома: «Это был не я»;
- Таня: «Это была не я».
Известно, что только один из ребят сказал правду. Кто на самом деле разбил окно?
(А) Маша
(Б) Таня
(В) Петя
(Г) Рома
(Д) невозможно определить
Задача 15.
Андрей хочет записать целые положительные числа в каждую из пяти клеток так, чтобы произведения двух соседних чисел были такими, как указано на рисунке. Чему будет равна сумма пяти чисел, которые он запишет в клетки?
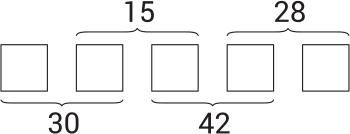
(А) 20
(Б) 24
(В) 30
(Г) 36
(Д) 40
Задача 16.
Фигура состоит из пяти прямоугольников. Лёша хочет раскрасить эти прямоугольники в три разных цвета так, чтобы любые два соприкасающиеся прямоугольника были раскрашены в разные цвета. Сколькими различными способами он может это сделать?
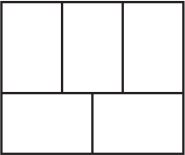
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 17.
Катя составляет башню из четырёх брусков, а затем меняет бруски местами. За один раз она может взять один или несколько брусков с верхней части башни и перевернуть их вверх ногами, как показано на верхнем рисунке. Какое минимальное количество раз Катя должна перевернуть бруски, чтобы получить из башни 1 башню 2?
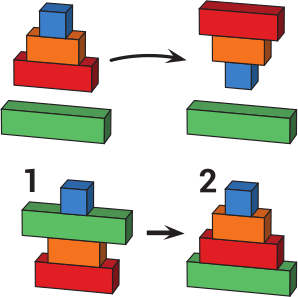
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 18.
Заяц, бобр и кенгуру соревнуются в прыжках по кругу. За один прыжок бобр перемещается на одно деление, заяц – на два деления, а кенгуру – на три деления. Они начали соревнование в точке «Старт». Победителем станет тот, кто окажется в точке «Финиш» за меньшее количество прыжков. Кто выиграет соревнование?
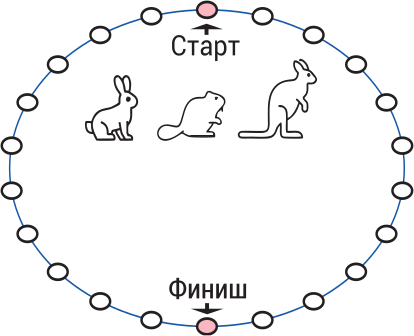
(А) бобр
(Б) заяц
(В) кенгуру
(Г) заяц и кенгуру
(Д) бобр и кенгуру
Задача 19.
Лёня хочет, чтобы сумма чисел в белых ячейках равнялась сумме чисел в серых ячейках. Какие два числа ему нужно поменять местами?
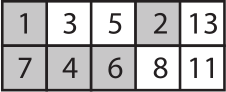
(А) 1 и 11
(Б) 2 и 8
(В) 3 и 7
(Г) 4 и 13
(Д) 7 и 13
Задача 20.
На рисунке изображено устройство, перемещающее ящики 1, 2, 3 и 4. Шестерёнка А вращается по часовой стрелке. Какие два ящика будут двигаться вверх?
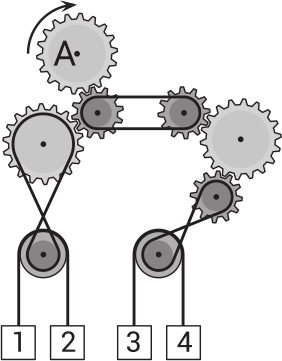
(А) 1 и 4
(Б) 2 и 3
(В) 1 и 3
(Г) 2 и 4
(Д) невозможно определить
Задача 21.
Толя рисует фигуры в шести ячейках пирамиды. Каждая ячейка верхнего и среднего рядов должна содержать все фигуры из двух ячеек, расположенных непосредственно под ней, и ничего больше. Какие фигуры Толя должен нарисовать в ячейке, расположенной посередине нижнего ряда?
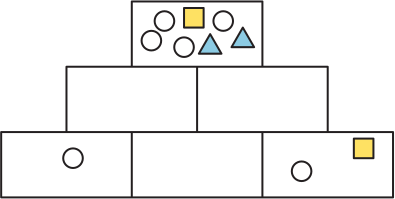
(А) 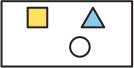
(Б) 
(В) 
(Г) 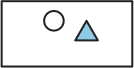
(Д) 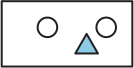
Задача 22.
У кенгуру есть два аппарата. Когда он кладёт лист бумаги в аппарат 1, лист разворачивается на 90° по часовой стрелке. Когда он кладёт лист в аппарат 2, на нем печатается изображение.

В какой последовательности кенгуру использовал аппараты, чтобы получить результат, как на рисунке?

(А) 2 - 1 - 1 - 1
(Б) 1 - 2 - 1 - 1
(В) 2 - 1 - 2 - 1
(Г) 1 - 1 - 1 - 2
(Д) 2 - 1 - 1 - 2
Задача 23.
Четыре столбика размещены вдоль 120-метровой дорожки. Какое наименьшее количество столбиков нужно добавить, чтобы дорожка оказалась разделена на участки одинаковой длины?
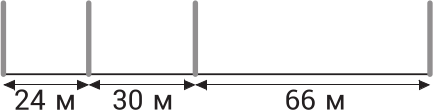
(А) 12
(Б) 15
(В) 17
(Г) 20
(Д) 37
Задача 24.
На столе стоит башня из блоков с номерами от 1 до 50. Лена строит из неё новую башню следующим образом: она берёт два блока с вершины исходной башни и кладёт их на стол в качестве основания новой башни. Затем она берет два верхних блока из оставшейся части исходной башни и кладёт их на вершину новой башни, и так далее, как показано на схеме. Какие два числа находятся на соседних блоках в новой башне?
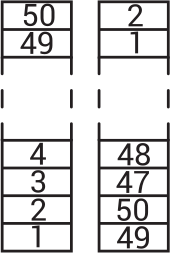
(А) 29 и 28
(Б) 34 и 35
(В) 29 и 26
(Г) 31 и 33
(Д) 27 и 30
Задача 25.
У Марины есть три карточки, на каждой стороне которых написано по одной цифре. На обороте карточки с цифрой 1 написана цифра 4, на обороте карточки с цифрой 2 написана цифра 5, на обороте карточки с цифрой 3 написана цифра 6. Марина в случайном порядке выкладывает карточки, а затем складывает три числа, которые видит на них. Сколько различных значений сумм может получить Марина?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 26.
В магазине две шляпы продаются по той же цене, что и пять юбок, три юбки – по той же цене, что и восемь футболок, а две футболки – по той же цене, что и три кепки. Какая из следующих покупок стоит дороже всего?
(А) шляпа и 5 юбок
(Б) шляпа, 3 юбки и кепка
(В) 8 юбок и 6 футболок
(Г) 37 кепок
(Д) 3 юбки и 3 кепки
Задача 27.
Соня и Рита играют в игру. Они могут поочерёдно убирать 1, 2, 3, 4 или 5 плиток из стопки плиток. Тот, кто уберёт последнюю плитку или плитки, проигрывает. В какой-то момент игры в стопке осталось 10 плиток, и настала очередь Сони убирать плитки. Сколько плиток Соня должна оставить Рите, чтобы быть уверенной в своей победе?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 28.
Какая из следующих фигур имеет максимальную площадь?

(А) A
(Б) B
(В) C
(Г) D
(Д) все имеют одинаковую площадь
Задача 29.
Исследователь хочет пройти через лабиринт от круга с отметкой «старт», до круга с отметкой «финиш». Он может двигаться только по горизонтали или вертикали, не может проходить через чёрные круги, а через любой белый круг может пройти только один раз. Если он хочет пройти через все белые круги, каким должен быть его следующий ход, когда он дойдёт до кружка, отмеченного крестиком?
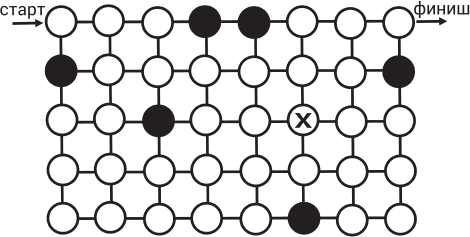
(А) 
(Б) 
(В) 
(Г) 
(Д) нет такого пути
Задача 30.
Учитель написал на доске целые числа от 1 до 15. Затем он разбил их на пять групп по три числа в каждой группе. Суммы чисел в первых четырёх из этих групп: 25, 27, 30 и 31 соответственно. В какой из групп содержится число 4?
(А) в первой
(Б) во второй
(В) в третьей
(Г) в четвёртой
(Д) в пятой

